Module 6
1. Module 6
1.9. Page 4
Module 6: Triangles and Other Polygons
Bringing Ideas Together
In the Explore section you investigated another method of sketching similar polygons. You also reviewed the relationships among angles and among sides of similar polygons.
For two similar polygons, the angles are equal in measure, and the sides are proportional—that is, the ratios of corresponding sides are equal.
 Self-Check
Self-Check
SC 5. How does the side proportion change for a similar polygon that is larger or smaller in size? Look at the similar polygons below.
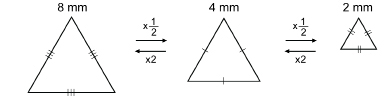
SC 6. The side proportion, or scale factor, moving between these triangles is shown. What do you notice about scale factor when you move from a large polygon to a small polygon? What does the scale factor look like as you move from a small polygon to a large polygon?
The following example determines if two figures are similar by comparing angle measurements and finding side ratios and scale factor.
Example 1
Are square floor tiles measuring 9 in on a side similar to square floor tiles measuring 1 ft on a side?
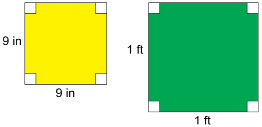
Solution
The corresponding angles are all right angles. So, the corresponding angles are equal in measure (congruent). A ratio is a comparison of two numbers. Make sure the units of all measurements are the same. If they are not the same, you will have to convert to a common unit. You have to use the same unit in both parts of the ratio.
Remember 1 ft = 12 in. So, the ratio of each pair of corresponding sides ![]()
Reduced to lowest terms, this ratio ![]()
Because corresponding angles are equal in measure and the sides are proportional, the squares are similar polygons.
Note that the scale factor describing the change from a 9-in square into a 12-in (1-ft) square is ![]()
![]()
Regular Polygons
regular polygon: a polygon with all its angles equal in measure and all its sides equal in measure
Did you know that some shapes are always similar to each other? All squares are similar. Squares are examples of regular polygons.
Equilateral triangles are another example of regular polygons. Each angle of an equilateral triangle is 60°, because 3 × 60° = 180°.
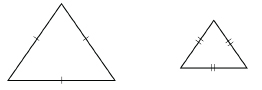
Can you think of another example of a shape that is always similar?
 Self-Check
Self-Check
SC 7. By what scale factor would you have to multiply the sides of an equilateral ![]() to obtain
to obtain ![]()
SC 8. The kitchen in Jasper’s home is rectangular in shape and is 12 ft by 9 ft. Jasper’s bedroom is also rectangular and is 8 ft by 10 ft. Are the two rooms similar polygons?
Similarity
In the next example, you will investigate whether the given pentagons are similar.
Example 2
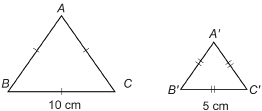
Determine the ratios of the pairs of sides of the pentagons ABCDE and ![]() Are the pentagons similar? Why or why not?
Are the pentagons similar? Why or why not?
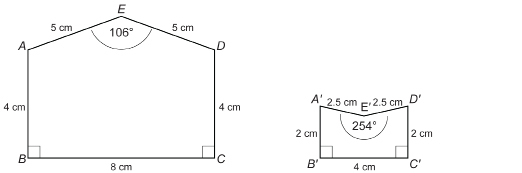
Solution
Find the ratios of the sides.
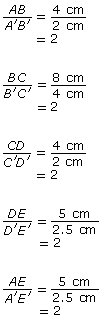
The ratios of the sides are equal, but the figures are not similar. The corresponding angles are not equal, since 106° is not equal to 254°.
In the next examples you will find the missing sides of two similar figures by solving proportions.
Example 3
In the diagram ![]() the measurements of side lengths are shown in units. For example,
the measurements of side lengths are shown in units. For example, ![]() has a measure of 2 units.
has a measure of 2 units.
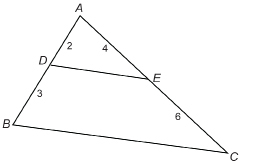
Is ![]() Give reasons for your answer to this question.
Give reasons for your answer to this question.
View “Example 3 Solution: Similar Triangles.”
Example 4
Two similar triangular city lots are pictured below. Find the missing measures x and y.
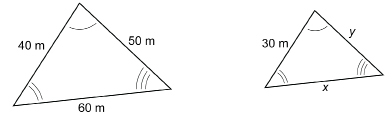
View “Example 4 Solution: Finding Lengths in Similar Triangles.”
Example 5
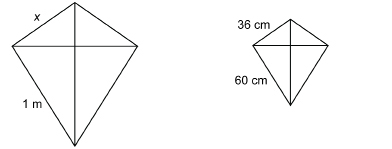
The outlines of two kites are similar polygons. Determine x.
Solution
Did You Know?

The Chinese were making kites from silk and bamboo 2800 years ago!
Remember that 1 m = 100 cm. Set up the proportion.
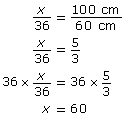
So, x = 60 cm.
Now it’s your turn.
 Self-Check
Self-Check
SC 9. Dorothy is preparing to sew an outfit for her toddler. She wants to adapt the following pattern.
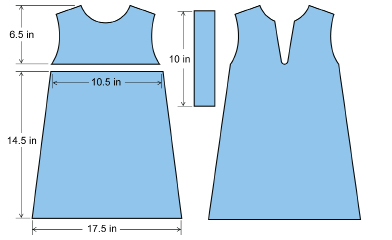
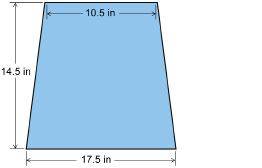
To fit her child, Dorothy plans to reduce the dimensions of the pattern by 10%. What is the scale factor? What will the dimensions of this section be if Dorothy decides to round each measurement to the nearest quarter inch?
SC 10. Shawn was writing a report about the World Cup held in South Africa in 2010. Shawn had to decide between two sizes of the South African flag for his report.
The length of the smaller flag is missing. Calculate the length to one decimal place.

© Gino Santa Maria/1215500/Fotolia
SC 11. Maxine is interested in model aircraft. She wants to build a ![]() scale model of the Silver Dart, the first powered airplane to fly in Canada.
scale model of the Silver Dart, the first powered airplane to fly in Canada.

<http://www.airforce.forces.gc.ca/v2/equip/hst/silverdart-eng.asp>; National Defence. Reproduced with the permission of the Minister of Public Works and Government Services, 2010
If the wingspan of the Silver Dart is 15 m, what will the wingspan of Maxine’s model be? Round to two decimal places.
Did You Know?
The original Silver Dart was made of steel tubing, bamboo, wire, and wood.
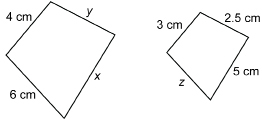
SC 12. The following polygons are similar. Find the missing measures (x, y, and z). Round to one decimal point.
 Mastering Concepts
Mastering Concepts
Answer this question. When you are finished, check your answer.
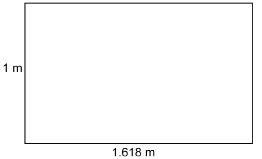
One rectangle that often appears in art and architecture is the golden rectangle. The proportions of the golden rectangle are considered pleasing to the eye. The length of the golden rectangle is approximately 1.618 times as long as it is wide. So, if the width is 1 m, the length would be 1.618 m.
One of the interesting properties of the golden rectangle is that if you draw a square inside with the width as one side, the rectangle remaining would also be a golden rectangle.
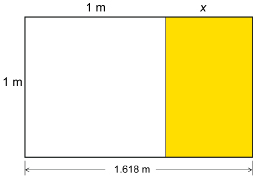
Assuming the large golden rectangle is similar to the smaller golden rectangle on the right, use a proportion to find x, correct to 3 decimal places. Does this value of x make sense in the diagram? Why?
Like squares, all equilateral triangles are similar; all regular pentagons are similar, and so on. You may also have thought of all regular octagons, hexagons, heptagons, and so on.