Module 7
1. Module 7
1.14. Page 4
Module 7: Trigonometry
Bringing Ideas Together
In Explore you examined the ratio in a right triangle of the side opposite to the hypotenuse of a given acute angle. This ratio is another example of a trigonometric ratio. You saw that, for similar right triangles and a particular acute angle, the ratio ![]() was the same value regardless of the size of the right triangle.
was the same value regardless of the size of the right triangle.
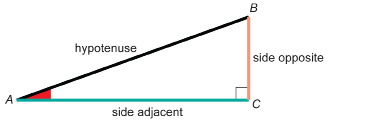
This ratio is called the sine ratio.
The sine ratio is always in relation to an acute angle (in this case, it is ∠A). You must identify the acute angle when you write the sine ratio in a particular situation.
So, sine ∠A = ![]() .
.
It is often written more simply as sin A = ![]() where A = measure of ∠A.
where A = measure of ∠A.
Example 2
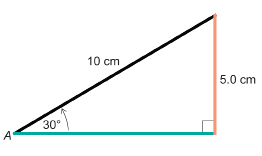
Draw a right triangle with an acute angle of 30°. Determine sin 30° to two decimal places.
Solution
It does not matter how large you draw the triangle, as all right triangles with a 30° angle will be similar in shape. However, a hypotenuse of 10 cm will make the calculation easier.
Once you draw the triangle, measure the opposite side and hypotenuse to the nearest millimetre.
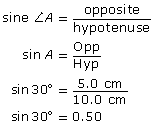
A ratio of 0.5 means that, in a right triangle with a 30° angle, the opposite side will be one half the length of the hypotenuse. For instance, if the opposite side were 30 in, the hypotenuse would be 60 in long, and ![]()
Example 3
Determine sin 45°, correct to two decimal places, by measuring the sides of a right triangle.
Solution
Draw a suitable right triangle. You may wish to draw a right triangle with a hypotenuse of 10 cm to simplify the calculation. Then measure the opposite side.
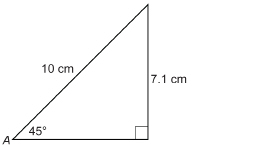
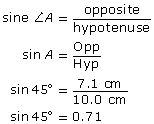
Note that the answer is only approximate, since measurements were only correct to the nearest millimetre.
This ratio means the opposite side is shorter than the hypotenuse and is 0.71 times as long. So, if the hypotenuse were 20 cm long, the opposite side would be about 20 × 0.71 cm = 14.2 cm long.
 Self-Check
Self-Check
Use the method of the previous two examples to complete the following table. You may wish to use 10 cm for the hypotenuse.
SC 5. Complete the following table.
|
Angle |
Hypotenuse |
Side Opposite |
Sine |
|
10° |
|
|
sin 10° = |
|
20° |
|
|
sin 20° = |
|
30° |
10 cm |
5.0 cm |
sin 30° = 0.50 |
|
40° |
|
|
sin 40° = |
|
45° |
|
|
sin 45° = 0.71 |
|
50° |
|
|
|
|
60° |
|
|
|
|
70° |
|
|
|
|
80° |
|
|
|