1. Lesson 4

1.8. Explore 4

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

You have been looking at points that lie at the intersection of a terminal arm of an angle and the unit circle. You can also look at points that are on a terminal arm of an angle but are not on the unit circle.


textbook

Read “Example 5” on page 200 in the textbook. Note the following while reading.

  • The coordinates of point A are the values of x and y on the triangle.
  • To determine r, use the Pythagorean theorem to solve
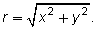
  • The radius, r, is always positive because it is a length without a direction.
  • There are six trigonometric ratios you have to determine.
Self-Check 3
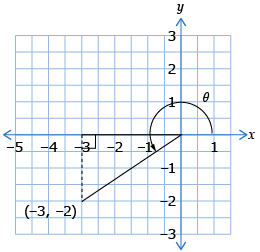
  1. The point A(−3, −2) lies on the terminal arm of an angle θ in standard position. Determine the values of csc θ and sec θ. Leave your answer as a fraction. Explain your process.

     
    This is a diagram of point A negative 3, negative 2, labeled with angle theta in standard position.
    Answer
  2. Determine the value of cot θ when 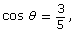 where 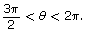Sketch a diagram to help determine the exact value. Leave your answer as a fraction. Answer

 

textbook

  1. Complete question 12.b. on page 202 in the textbook. Answer

You have looked at finding trigonometric ratios when given a point on the terminal arm of an angle in standard position. How can you determine trigonometric ratios when only given an angle?

 

In Mathematics 20-1 you used reference triangles of 30°-60°-90° or 45°-45°-90° to help determine the exact values for trigonometric ratios for multiples of these angles. The unit circle can assist you in determining the exact values for trigonometric ratios as well. You will determine six different trigonometric ratios for angles measured in degrees and radians.



Look at what quadrant θ is in, and determine if the x-value of the point should be positive or negative.