1. Module 7

1.25. Page 3

Mathematics 10-3 Module 7 Lesson 5

Module 7: Trigonometry

 

Explore

In previous lessons you explored the sine and tangent ratios. For a given acute angle in a right triangle, the tangent ratio was defined as , and the sine ratio was defined as .

 

You discovered that, for similar triangles, the values of the tangent ratios were the same regardless of how large or small the right triangles were. This was also true for the sine ratio. So, if you knew the angle, you could determine the ratio. And, if you knew the ratio, you could determine the angle.

 

Try This

 

In this activity you will explore one more trigonometric ratio. This ratio involves a different pair of sides within a right triangle. You will explore this ratio for a variety of right triangles with the same angle. For this comparison you will use the skills for similar right triangles that you mastered in Module 6.

 

You will need your ruler, a protractor or square, and a calculator. Work with a partner, if possible.

 

Consider the right triangles in the following diagram.

 

 

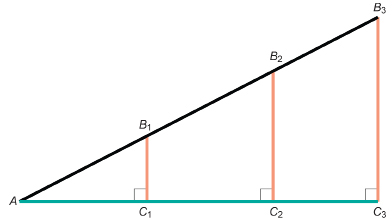
This illustration shows a right triangle AB3C3;. Angle C3 is a right angle. B1 and B2 are points on side AB3, with B1 closer to A than B2. Points C1 and C2 are points on side AC3. B1C1 is perpendicular to AC3, as is B2C2. The base AC3 is green with all sides B1C1, B2C2, and B3C3 orange.

 

Step 1: Draw a diagram like the previous one. Your diagram doesn’t have to be the same size, and ∠A can be of any measure.

 

Step 2: Record all of the following information in the table.

 

For right triangle AB1C1, measure to the nearest millimetre and record the length of sides AC1 and AB1.

For right triangle AB2C2, measure to the nearest millimetre and record the length of sides AC2 and AB2.

For right triangle AB3C3, measure to the nearest millimetre and record the length of sides AC3 and AB3.

 

Right Triangle

Side Adjacent ∠A (nearest mm)

Hypotenuse
(nearest mm)

(2 decimal places)

ΔAB1C1

AC1 =

AB1 =

ΔAB2C2

AC2 =

AB2 =

ΔAB3C3

AC3 =

AB3 =

 

TT 1. Explain why ΔAB1C1, ΔAB2C2, and ΔAB3C3 are similar triangles.

 

TT 2. Because the triangles are similar, the ratio you calculated should be the same for each triangle. The following statements prove these ratios for ΔAB1C1 and ΔAB3C3 are equal. Supply a reason for each step in the proof.

 

Statement

Reason

 

 

.

 

 

Share

 

Share your answers from the Step 2 table in Try This with as many other students as possible. You may find that the ratios for your triangles were different from the ratios obtained by other students. Why? Measure ∠A in your triangles, and compare this angle measurement with other students. Can you identify a pattern between the ratio calculated for the different angle measures?

 

Summarize the patterns you noticed during this Share activity, and save a copy to your course folder.