Lesson 1

Explore

In Try This 1 you began to explore a simple rational function. A rational function f(x) is a function that can be written as , where g(x) and h(x) are polynomial functions and h(x) ≠ 0.

The rational function from Try This 1 can be written as  and has the same typical shape as a function of the form . This function has a vertical asymptote at x = 0 and a horizontal asymptote at y = 0. This is because, if you rewrite the function as x × y = a, you realize that neither x nor y can equal zero if a is a non-zero number. Watch Rational Function Asymptotes to explore the asymptotes.

It is possible to transform rational functions just like other functions? Try This 2 explores this idea.

Try This 2

1. In Module 1 you used the general formula y = af[b(x − h)] + k to help graph functions similar to y = f(x) using transformations. Explain how 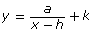 can be thought of as a variation of y = af(x − h) + k.
2. Predict the effects of changing a, h, and k in .
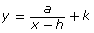3. Open Transforming a Rational Function and check your solutions to question 2.
   
   
    
   
   
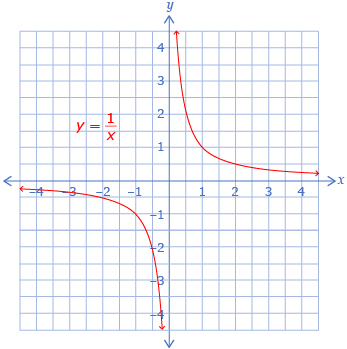
4. The function 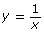 is shown.
   
   
    
   
   
   Describe how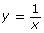  can be used to graph the following functions using transformations:
   
   1. 
   2. 
   3. 
   4. 
      
5.  Use Transforming a Rational Function, if needed, to help answer the following questions.
   1. Predict where asymptotes will occur in 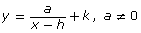 in terms of a, h, and k.
   2. Explain how you can determine the domain and range of 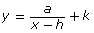in terms of a, h, and k.

Save your responses in your course folder.