Lesson 1

So far, you have experimented with rational functions of the forms  and In Try This 3 you will investigate graphing slightly more complex rational functions using transformations.

 

Try This 3

1. Carolina is planning on graphing the function 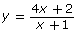 by hand using transformations. She completes the following steps:
   
   
    
   
   
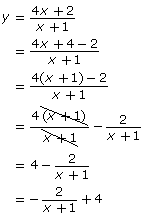
   Explain why Carolina changed the format.
2. Although Carolina’s method is correct, the method will typically only work with rational functions that include a linear polynomial in the numerator and denominator. Describe two other methods you could use to graph the function
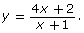
3. Explain whether the methods you described in question 2 will allow you to graph the following rational functions:
   • 
   • 
   • 
4.  
   1. Graph the functions from question 3 using technology; then use your graphs to complete a table like the following.
      
      

      Function
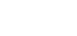
      Non-permissible Value(s)
      Vertical Asymptote(s)
      Horizontal Asymptote(s)
      x-intercept(s)
      y-intercept(s)
      Domain
      Range
      End Behaviour

      
      
   2. Describe any similarities and/or patterns you notice between the graphs of the three functions.

Save your responses in your course folder.

 

Share 2

With a partner or group, discuss the following questions based on your graphs created in Try This 3.

1. Describe why a graphing strategy that uses transformations may be more difficult to use for rational functions than some of the other functions used in this course.
2. Compare the patterns you saw in question 4. Do you expect these patterns will hold for all rational functions? Explain.

If required, save a record of your discussion in your course folder.