1. Lesson 6

1.4. Explore 3

Mathematics 30-1 Module 7

Module 7: Rational Functions and Function Operations

 

When determining the domain and range of a composition of functions, you need to pay attention to what happens at each step.

 

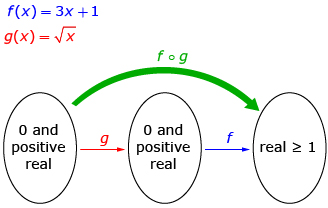
Two functions are given. One function is f at x equals 3 x plus 1, and the other function is g at x equals the square root of x. Function g goes from 0 and positive real numbers to 0 and positive real numbers, and function f goes from 0 and positive and real numbers (function g’s range) to real numbers greater than or equal to 1. The composition f composed with g at x goes from 0 and positive real numbers to real numbers greater than or equal to 1.

The function can use only an input of 0 or positive real numbers and can give only an output of 0 or positive real numbers, so its domain is x ≥ 0 and its range is g(x) ≥0. Using 0 or positive real numbers, the function f(x) = 3x + 1 can give only an output of real numbers greater than or equal to 1. Thus, the domain of (f o g)(x) is x ≥ 0 and the range is (f o g)(x) ≥1.


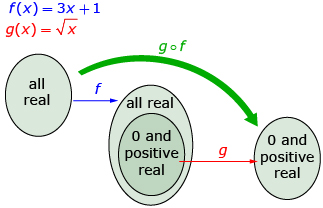
Two functions are given: The function f at x equals 3 x plus 1 is shown in blue, and the function g at x equals the square root of x is shown in red. The diagram shows an oval labelled all real, with a blue arrow labelled f leading to a second oval also labelled all real. Inside the second oval is a third oval labelled 0 and positive real. A red arrow labelled g goes from this third oval to a final oval labelled 0 and positive real. In addition, a green arrow goes from the first all real oval to the final 0 and positive real oval. The green arrow is labelled g composed with f.

The function f(x) = 3x + 1 has a domain of any real number and a range of any real number. However, the function can use only 0 and positive real numbers as an input and will give only 0 and positive real numbers as an output. Thus, the domain of is limited to x-values that will give f(x) ≥ 0 and is The range of is



assessment

Read “Example 2” on pages 502 and 503 of the textbook to see another example of how the domain and range can be determined for a composition of functions. Note how any domain restrictions on the inner function as well as the outer function must be taken into consideration and combined to get the domain of the composite function.

 

Self-Check 2
  1. Complete “Your Turn” from “Example 2” on page 503 of the textbook. Answer
  2. Complete questions 4.c., 4.d., 4.e., and 8 on page 507. Answer