Lesson 4

In Try This 2 you may have found that each row of Pascal’s Triangle can be determined by adding adjacent numbers in the preceding row.

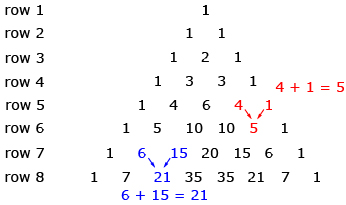
You may have noticed some of the following patterns:

• Each row is symmetrical.
• Row n has n numbers in it.
• The second number of the row is equal to n − 1.
• The sum of row n is 2n − 1.

Although Pascal’s triangle has many interesting patterns, the pattern of the triangle’s construction is most important for this lesson.

To expand a more complex binomial, such as (3q2 − 5j)n, simply treat 3q2 as a single unit and −5j as a single unit. Alternatively, you can expand (x + y)n and, in the expanded version, replace x with 3q2 and y with −5j.

The coefficients of the binomial (x + y)n can be determined using row n + 1 of Pascal’s triangle. To determine the expansion of (x + y)7, use row 7 + 1, or row 8, of the triangle to determine the coefficients. Watch Binomial Expansion with Pascal’s Triangle to see a complete description of how to expand (x + y)7.

Self-Check 1