1. Lesson 1

1.3. Explore 2

Mathematics 30-2 Module 3

Module 3: Permutations, Combinations, and the Fundamental Counting Principle

 

In “Investigate the Math” question G, which you completed as part of Try This 2, you were asked to create an expression relating the number of routes between

  • Winnipeg and Regina, a
  • Regina and Saskatoon, b

For each of the 3 routes between Winnipeg and Regina, there were 2 routes from Regina to Saskatoon. This is represented by a • b. That means that there were 3 × 2 or 6 ways from Winnipeg to Saskatoon, initially, and 4 × 3 or 12 ways once the new routes were added.

 

 

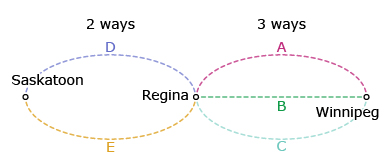
This diagram shows two routes from Saskatoon to Regina labelled D and E and three routes from Regina to Winnipeg labelled A, B, and C.

There are 3 x 2 = 6 ways to travel from Winnipeg to Saskatoon.

 

 

 

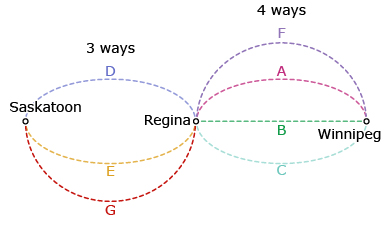
This diagram shows three routes from Saskatoon to Regina labelled D, E, and G. It also shows four routes from Regina to Winnipeg labelled F, A, B, and C.

There are 4 x 3 = 12 ways to travel from Winnipeg to Saskatoon once the new routes have been added.

 

 

The fundamental counting principle explains that if there are a ways to complete one task and b ways to complete another task, then there are a • b ways to complete the two tasks.


 

Think back to the example from Discover at the start of this lesson. At Louie’s Bistro, there were 2 salads, 4 entrées, and 3 desserts from which to choose a three-course meal. Using the fundamental counting principle, you can calculate the number of possible meals.

 

 

2 × 4 × 3 = 24 meals



textbook

If you would like to see another example of how a tree diagram and the fundamental counting principle are used to determine the number of outcomes, read through “Example 1” on page 68 of your textbook.

 

 

Self-Check 1
  1. Kenton is choosing an outfit to wear for the day. He has a choice of 5 pairs of slacks and 8 different shirts. How many different outfits can he choose? Answer

    This is a photo of a man getting dressed with clothes nearby.
    Jupiterimages/Brand X Pictures/Thinkstock
  2. Use the following information to find the possible number of menu combinations.

    The graduation council has been given the task of determining the menu for the graduation banquet. They have to select one salad, one main course, one side dish, one vegetable dish, and one dessert from the following choices.

    • salad: Caesar, garden, tomato-herb, pasta
    • main course: chicken, beef, fish
    • side dish: rice, baked potato, mashed potato, French fries, noodles
    • vegetable: peas, corn, carrots, mixed vegetables, broccoli
    • dessert: cheesecake, pudding, ice cream, pie


    Answer
  3. How many routes are there from point A to point B if each path must take you closer to B?

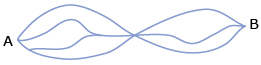
    This image shows routes from point A to point B.

    Answer

 

textbook

  1. Complete “Your Turn” on page 68 of your textbook. Answer