1. Lesson 3

1.3. Explore 2

Mathematics 30-2 Module 3

Module 3: Permutations, Combinations, and the Fundamental Counting Principle

 

This is a photo of a pile of Scrabble game tiles.

Hemera/Thinkstock

In Try This 2, you may have found that the problem can be represented by

 

When generalized for n objects taken r at a time, the total number of permutations is .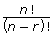



In the next Try This, you will use the tile data you collected in Discover to work with the permutations formula.

 

Try This 3

 

Retrieve your chart from Try This 1. Add one extra column, to the chart as shown.

 

Number of Tiles in Box

Number of Draws from Box

Total Number of Possible Permutations

List Possible Permutations

2

2

2

AE, EA

 

2

1

2

A, E

 

3

3

 

 

 

3

2

 

 

 

3

1

 

 

 

4

4

 

Do not list.

 

4

3

 

Do not list.

 

4

2

 

Do not list.

 

4

1

 

 

 

5

5

 

Do not list.

 

5

4

 

Do not list.

 

5

3

 

Do not list.

 

5

2

 

Do not list.

 

5

1

 

 

 
  1. Determine which column represents n and which column represents r.
  2. Complete the chart by calculating 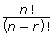 for the remaining rows. Show your work.  
  3. In what instances could n! only be used to calculate the number of permutations, and when must 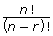 be used? Provide an example from the chart.

course folder Save your responses in your course folder.

0! is defined as 1.
The variable n is the total number of elements you could choose from. The variable r is the subset—that is, the number of tiles used to create the permutations.