Lesson 3

When presented with permutation questions, it is important to be able to identify n (i.e., the total number of objects there are to select from) and r (i.e., the number of objects being selected each time). Some questions will require you to do a little deciphering of the wording to find these values.

 

Consider the following scenario: There are 6 people boarding an empty bus that has 30 seats. In how many different ways may the people be seated?

 

If you would like to solve this by drawing blanks, draw your blanks for the elements that are most restricted. In this case, there are fewer people than seats; so draw the blanks to represent each person and then fill in the blanks with the number of seats they may choose from.

 

bus: iStockphoto/Thinkstock

 

Since the first person who gets on the bus has 30 seats to choose from, 30 is placed in the first blank. Now that a seat is taken, the second person has 29 seats to choose from, and so on.

 

Completing this solution by filling in all of the blanks, you get 30 × 29 × 28 × 27 × 26 × 25 or 427 518 000 ways.

 

If you chose factorial notation to solve this question, you would use the following formula:

 

 

In this example, n is 30 and represents the total number of seats; and r is 6 and represents the number of people who choose a seat. You are finding the number of ways of choosing 6 items (r) from 30 items (n). Using the formula, you would get the following:

 

 

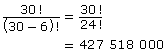
Drawing blanks and determining the number of ways they could be filled works well when there is a small number of items being arranged; however, if there is a large number of items to be arranged, drawing blanks can be a tedious and time-consuming method.

 

For example, imagine that 100 people line up for 50 audition spots on a talent show. In how many ways can the 50 audition spots be filled? You could draw 50 blanks and work to fill them in, but you also know a formula that can be used to determine the number of permutations.

 

There are a total of 100 items, so n = 100. From these 100 items, only 50 are taken at a time, so r = 50. Use the formula to calculate the number of permutations.

 

 

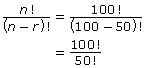
You may recall that 69! is the largest factorial that can be calculated using a calculator. To get around this issue, many graphing calculators are programmed to determine the number of permutations using a different notation, nPr, where

• n is still the total number of objects
•  r is the number of objects you want in each arrangement

To calculate  you would use 100P50.

 

Investigate how to perform this on your calculator. You may need to reference the calculator�s guide or ask your teacher for assistance.

 

Self-Check 2