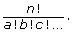Lesson 3
1. Lesson 3
1.10. Explore 9
Module 3: Permutations, Combinations, and the Fundamental Counting Principle
From doing Try This 4, you may have discovered that the number of permutations of n objects where r are identical, another s are identical, another t are identical, and so on, is 
Now go back and think about the example with Sara and Mark. Why did they get different answers even though they have the same number of letters in their names? Sara has 12 arrangements since the letter A is used twice in her name. She could find the number of arrangements by using the repetitions formula 
Mark has no repeating letters, so the number of arrangements he can find is 4! or 24.
The idea of repeated elements can be used in other permutation problems as in the next Try This.
Try This 5
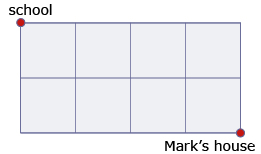
After their math class, Sara and Mark are going to his house to study for an upcoming math test. They wonder if they can use the concepts they learned in math class to figure out the number of routes they have to choose from in order to get from the school to his house. Mark’s house is 4 blocks east and 2 blocks south of the school. Since they don’t want to travel any extra distance, Sara and Mark plan to walk only east or south. Can you help them determine the number of routes?
If you need a little assistance figuring this question out, read “Example 3” on pages 102 and 103 of your textbook.
Save your responses in your course folder.
Self-Check 6
- Complete “Your Turn” on page 103 of your textbook. Answer
- Complete questions 6, 12, 13, and 17 on pages 105 to 107 of your textbook. Answer
Add the following to your copy of Formula Sheet:
- permutation formula: Permutations of n objects taken r at a time formula is represented by nPr where 0 ≤ r ≤ n and
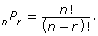Remember that 0! is defined as 1. - repetition formula: The number of permutations of n objects when a, b, c, and so on, objects are identical, is
