Lesson 1

To simplify a rational expression means to write an equivalent expression where the greatest common factor between the numerator and the denominator is 1. Such an expression is described as being in simplified form or reduced to lowest terms.

 

The following example shows how you can simplify a rational number by using the method of prime factorization. Pay careful attention to the steps of this example. You will apply these steps to rational expressions in Try This 4 later in this lesson.

 

Example

1. Simplify 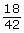 by using prime factorization.
2. Verify that the simplified form is equivalent to the original rational number.

Solution

1. 
   
   

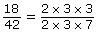
   	Use prime factorization to write out all the factors of the numerator and denominator.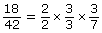
   	The expression can be written as the product of three fractions.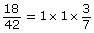
   	Since the first two fractions are equal to 1, the expression can be simplified.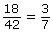
   	Using the property of 1, the expression is again simplified.

2. According to the property of 1, where any number multiplied by 1 is equal to itself,
   
   
    
   
   
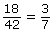
   You can verify this by putting each side into your calculator, and the answer should be the same.

In Try This 1, you found that by applying a series of mathematical operations to a number, you end up with a number that is 2 less than the original number. The following statement summarizes this observation.

 

 

The expression  is equivalent to the expression x − 2 for all values of x, except when x = −2.

 

In Try This 4, you will use the same principles demonstrated in the previous example to verify the result.

 

Try This 4

1. Consider the rational expression 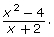Show that this expression simplifies to x − 2.

2. Simplify the rational expression 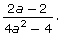State any non-permissible values.

Save your responses in your course folder.

 

Share 3

 

In a group or with a partner, answer the following questions.

1. What are some key differences between simplifying rational numbers and simplifying rational expressions?
2. Why is it necessary to include the non-permissible value(s) with the simplified form even though this form may not have a denominator?
3. Based on your answer to question 2, when should you identify non-permissible values?

If required, save a record of your discussion in your course folder.