Module 6
1. Module 6
1.24. Page 2
Module 6—Mendelian Genetics: The Transmission of Traits to the Next Generation
 Explore
Explore
 Read
Read

© Chistoprudov Dmitriy Gennadievich/shutterstock
Probabilities are usually expressed as real numbers with values from zero to one, for example 0.00–1.00. You may also express probabilities as fractions or percentages. A probability of zero means “no chance,” while a probability of one means it’s a “sure thing.” Anywhere in between, the chance will differ; low values indicate it is unlikely, high values indicate it is likely. There are two general rules when considering probability. They are the rules of addition and product. Deciding when to use which rule depends on whether the probabilities are linked or independent.
Addition Rule
If two outcomes are mutually exclusive (you can have one but not the other), the probability that either will occur is their sum.
Dice Example
- The probability that you will roll a 3 on a single die is
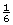 (6 for the 6 sides, or possibilities).
(6 for the 6 sides, or possibilities).
- The probability that you will roll a 4 is the same (
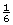 ).
).
- Thus, the probability that you will roll either a 3 or a 4 is
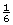 +
+ 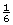 =
= 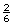 or
or 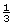 , or o.33, or 33%.
, or o.33, or 33%.
Having many exclusive outcomes makes the likelihood, or probability, increase.
Multiplication Rule
If two outcomes are independent (not linked), the probability that both will occur is their product.
Dice Example
- The probability that you will roll a 6 on a single die is
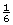 , and the probability that you will roll a 6 on a second die is the same.
, and the probability that you will roll a 6 on a second die is the same.
- However, the probability that you will roll two sixes on a pair of dice (at once) is
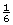 x
x 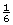 =
= 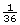 , or 0.03, or 3%.
, or 0.03, or 3%.
Having many independent outcomes occur at once makes the likelihood, or probability, decrease.
Example
What is the probability of three coin tosses coming up heads, tails, and tails?
Which rules will be applied?
- The multiplication rule will be applied.
How will it be applied?
- Take the probability of the first event, times the second, times the third.
So what is the probability of heads, tails, tails in a coin toss?
- (
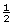 ) x (
) x (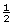 ) x (
) x (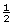 ) =
) = 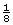 chance or 0.125 or 12.5%
chance or 0.125 or 12.5%
Note: Probability questions are common numerical response questions on your Diploma Exam. There isn’t an opportunity to record numerical responses as fractions, but the question can request your answer as a decimal, or as a percent. Read the question carefully—there’s a big difference in recording 0.125 or 12.5% in a machine-scored response.
 Watch and Listen
Watch and Listen
Return to the video on Classical Genetics and Dihybrid Crosses. Using the navigation bar on the right edge of the video, start watching the section titled “Bio Bit: Dihybrid Crosses in Canaries.” Continue viewing until the end of the video. Answer the following questions and save your work in your course folder. You may consult with your teacher to verify your answers.
TR 1. What is the probability of rolling a 3 on one die?
TR 2. What does the sum of all possibilities equal?
TR 3. What is the probability of rolling a 6 on two different dice at the same time? To figure this out, what “rule” did you need to use?
TR 4. How can you use this rule and two smaller Punnett squares to predict the offspring of a dihybrid cross?
TR 5. If you assume that the parents are heterozygous for all three traits in the film, what is the probability of having a child with widow’s peak, hitchhiker’s thumb, and free earlobes?
 Lesson 5 Lab—Calculating Probability
Lesson 5 Lab—Calculating Probability
Probability can be defined as a study of the chance that certain events or phenomena will happen. In this lab, you will explore how probabilities with coin tosses can be either linked or not linked. You will then draw connections between the outcomes of coin tosses with the outcomes of genetic crosses.
Complete the lab and activities on calculating probability. You will then be prompted to complete the Module 6: Lesson 4 Assignment as part of the lab.