Unit 2
Page 3
Unit 2: Circle Geometry
Connect
central angle: an angle with its vertex at the centre of a circle
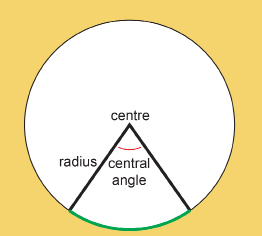
The sum of the central angles of a circle is 360°. Dividing 360° by the number of equal spaces between the spokes of your medicine wheel will calculate the central angle measurements. The spokes on either side of the central angle would be the two radii. (Remember that the term radii is the plural form of radius.)
Go to Central Angle at the Mathematics Glossary website.
A medicine wheel with four evenly spaced stone spokes would have central angles measuring 90°. Three spokes joining the central cairn and surrounding circle would form 120° central angles.
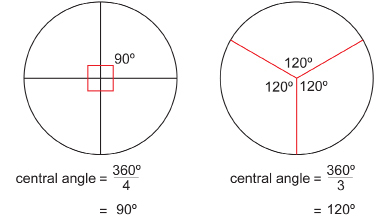
In both medicine wheels, the sum of the central angles is 360°.
 Building Understanding
Building Understanding
You know from previous investigations that the sum of the central angles in a circle is equal to 360°. As well, you know that the diameter of a circle is a straight line running through its centre. Watch the Circle Diameter animation. Pay close attention to the angle measure of the diameter.
straight angle: an angle with a measure equal to 180°
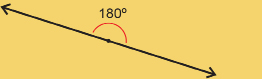
The animation shows that the diameter cuts the circle into two sections. Half of 360° is 180°. So the diameter has a straight angle measuring 180°.
Go to Straight Angle at the Mathematics Glossary website. If you feel you need further review, go to Refresher on Types of Angles.
This lesson presents many terms. Some of these terms you have seen in previous mathematics courses. Some of these terms will be new to you. If you haven’t done so already, now is a great time to start a foldable. You may want to create an angle foldable in addition to your circle geometry foldable. See page 376 of the textbook for detailed instructions on setting up your foldable.
Remember to add any new formulas to your formula sheet and new ideas to your foldable like the one on page 376 as well.