Page 4

Mathematics 9 Unit 2 Lesson 1

Unit 2: Circle Geometry

 

Math Chat
 

To complete this activity, you will need the medicine wheel you created in the Explore section of this lesson.

 

You may find it helpful to use different coloured rubber bands or pencils. This will help make identifying line segments and angles easier.

 

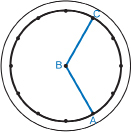
Step 1: Label the centre point of your medicine wheel point B.

 

Step 2: Choose the endpoint of a spoke on the surrounding circle of your wheel. Label this point A.

 

Step 3: Use a different colour of rubber band or pencil to connect point A to point B.

 

Step 4: Now choose another spoke on your circle that is at least two spokes away from point A. Label this point C.

 

Step 5: Use a rubber band or pencil to connect point A to point C.

 

These two spokes will create ∠ABC. An example arrangement of spokes is shown in the graphic that follows.

 

This illustration shows a geoboard with two lines drawn out from the centre point to the surrounding circle. This forms angle ABC.

 

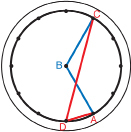
Next, pick another point on the medicine wheel. This point needs to be outside of the arc formed between point A and point C.

 

Step 1: Label this point D.

 

Step 2: Use a different colour of rubber band or pencil to connect point D to point A.

 

Step 3: Then use a rubber band or pencil to connect point D to point C.

 

These two line segments will create ∠ADC. An example arrangement of these line segments is shown in the graphic that follows.

 

This illustration shows a geoboard with two lines drawn from another point, labelled D, on the circle to point A and C.

 

Now compare the angles and line segments you created on the geoboard using the following as a guide.

  • Are line segments DA and DC radii? Why or why not?
  • How is ∠ABC similar to ∠ADC? How are they different? In your comparison, look at where the endpoints of each angle are on the surrounding circle. Also, compare the location of the vertex of each angle. The vertex of ∠ABC is at point B. The vertex of ∠ADC is at point D.

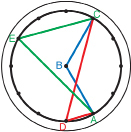
Label a fourth point on the medicine wheel point E. As before, this point also needs to be outside of the arc formed between point A and point C.

 

Step 1: Use a different coloured rubber band or pencil to connect point E to point A.

 

Step 2: Then connect point E to point C using a rubber band or pencil.

 

These two line segments will create ∠AEC. An example arrangement of these line segments is shown in the graphic that follows.

 

This is an illustration of a geoboard with two lines drawn from another point, labelled E, on the circle to point A and C.

 

Compare the angles you created on the geoboard using the following as a guide.

 

How is ∠AEC similar to ∠ADC? In your comparison, look at where the endpoints of each angle are on the surrounding circle. Also, compare the location of the vertex of each angle.

 

Post your findings to the discussion board. Respond to two other postings. Use the following questions to respond to other students.

  • Did other students call line segments DA and DC radii? If so, did you agree with this decision?
  • How is ∠ABC similar to ∠ADC and ∠AEC? How is it different from the other two angles?
  • What do ∠ADC and ∠AEC have in common?

Please keep your medicine wheel with its newest angles and line segments intact. You will be analyzing it further in this lesson.

 

In Math Chat you drew line segments DA, DC, EA, and EC between the endpoints of the spokes of your medicine wheel. Through your discussion with other students, you may have found that, although these line segments divided the circle, radius was not an appropriate term.

 

chord: a line segment with endpoints on a curve

 

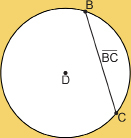
This is an illustration of a circle with centre D and a chord drawn from point B on the circle to point C on the circle.

The line segments did not connect the centre of the circle to a point on the circumference of the circle. Another term needs to be added to your math vocabulary. These line segments are known as chords because they connect two points on the circumference of the circle.

 

Go to Chord at the Mathematics Glossary website.

 

Self-Check
 

SC 2. Would line segments BA and BC on your medicine wheel be considered chords? Why or why not?

 

Compare your answers.

 

The chords in your medicine wheel create two other angles:

  • Chords DA and DC form ∠ADC.
  • Chords EA and EC form ∠AEC.

inscribed angle: an angle with its vertex on a circle and each arm intersecting the circle

 

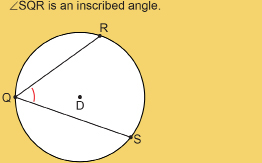
This is an illustration of inscribed angle SQR. This angle is formed by chords QR and QS, which share the common endpoint Q.

Since ∠ADC and ∠AEC are formed by chords that have their endpoints on the circle, they are known as inscribed angles.

 

Go to Inscribed Angle at the Mathematics Glossary website.

 

Looking at your medicine wheel, both ∠ADC and ∠AEC share the same arc with ∠ABC. Each angle has one arm that ends on point A of arc AC and one arm that ends on point C of arc AC. This means that ∠ABC, ∠ADC, and ∠AEC subtend the same arc. Each angle’s arms are formed by its vertex and the endpoints of arc AC.

 

Go to Subtend at the Mathematics Glossary website.

 

Now, view the animation titled Medicine Wheel Arc, which shows how ∠ADC and ∠AEC share arc AC with the central angle, ∠ABC.

 

So, ∠ADC is an inscribed angle subtended by the arc AC; ∠AEC is an inscribed angle subtended by the arc AC; and ∠ABC is a central angle subtended by the arc AC.