Lesson 4: Surface Area of 3-D Objects

Glossary Terms

In this lesson the suggested glossary terms to add are the following:

• 3-D object
• apex
• lateral area
• net
• prism
• pyramid
• regular polygon
• right cone
• right cylinder
• sector
• sphere
• surface area

-----------------------------------------------------------

Imagine taking a 3-D object and submerging it in a tub of water. The area of the object that is in contact with the water is called the surface area. You can also think of surface area as the measure of how much exposed area that a solid object has.

How would you determine the surface area of an object?

One way to do determine the surface area of the object is to peel off the outer layer of the object and then calculate the area of the peel. The peel is called the net. In Math Lab: The Surface Area of an Orange, you obtained a net of the orange (i.e., the orange peel sections) and added the areas of each part of the net (i.e., each peel section) to obtain the surface area of the orange.

As you move through this lesson, you will examine the nets of other 3-D objects. By adding together the sections of a net, you can determine the surface area of those objects.

Watch and Listen

Use "Surface Area of Prisms" to find out how to use the net of a rectangular prism to determine its surface area.

--------------------------------------------------------------------------

then watch “Surface Area of Prisms 2 ” to see another example of the net of a rectangular prism used to determine its surface area. 

-----------------------------------------------------------------------

Try This: Prisms, Pyramids, and Cylinders

Work with a partner (if possible) to examine the nets of prisms, pyramids, and cylinders. Use the following document titled Surface Area and Volume Investigation (or copy by hand) to summarize the information you will collect during this investigation. You may want to use the materials outlined in the Launch section as part of the investigation.

• paper
• prism net and pyramid net
• soup can with label
• scissors
• scotch tape
• a rectangular prism, such as a wooden block, a shoe box, or a cereal box
•  toblerone box if possible

For each 3-D object, create a net that can be easily folded into the 3-D object. To get started, you can use the following descriptions. However, you are not limited by the descriptions. You are free to use other ways of creating a net for the object.

Remember to add the information you discover to your “Surface Area and Volume Investigation” document. Then save a copy of your completed handout in your course folder.

Use the cereal box to create the net of a rectangular prism.

• Carefully unfold the cereal box and flatten it.
• Cut off any flaps that are not part of the surface area. (Some flaps will remain because they are a part of the exterior of the box.)

Use an empty Toblerone box to create the net of a triangular prism.

• Carefully unfold the box and flatten it.
• Cut off any flaps that are not part of the surface area.

To create a net of a square pyramid, go to Square Pyramid Net and print a copy.

• Cut out the net.
• Fold along the lines so it forms a three-dimensional pyramid.

Use the soup can with a label to create a net of a cylinder. For an idea of how you can do this, follow this procedure.

• Trace each circular end onto a sheet of paper.
• Cut out each of the ends.
• Remove the label from the soup can.
• Tape the circular ends to the label so that the net can be rolled into a 3-D cylinder.

Try This

TT 1. For each net, describe how many sections there are in the net.

TT 2. For each net, describe what dimensions will be needed to determine the areas of each section.

TT 3. For each net, describe what the formula for the surface area could look like. Try to match the formula below to each shape:

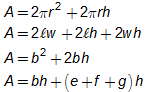
Use the link below to check your answers to Try This 1 - 3.

Possible TT1- 3 Solutions

Here is a great video that shows you how to find Surface Area of a Right Rectangular prism

Read

Read the textbook.

Self-Check

You have seen in the examples how a formula is applied in finding the surface area of a pyramid. Now use the formulas that you created to find the solutions to the following problems.

SC 1. Determine the surface area of the following pyramid, to the nearest in².

SC 2. Determine the surface area of the cylinder to the nearest cm².

Note the answer to SC2 is 150.8 cm². Typo in the answer.

SC 3. Determine the surface area of the following prism, rounded to the nearest cm².

SC 4. Consider the net shown. What does this net represent?

1. A cube with a side 10 cm.
2. A box with a length and width 10 cm and a height 5 cm.
3. A box with a length and width 5 cm and a height 10 cm
4. This net does not represent a box.

Compare your answers.

Mathematics 10C Learn EveryWare © 2010 Alberta Education