Lesson 9: Using Trigonometry to Find Missing Angles
Created by IMSreader
Explore
Module 1: Part 2 Trigonometry
 Try This 1
Try This 1
Complete the following in your binder.
1. Find the missing angles, given the following statements. Round your answer to the nearest degree.
a. sin M = 0.8290
b. cos Θ =0.0698
c. tan B = 1.1504
d. sin H = 4/5
e. cos Θ = 2/3
f. tan J = 2.2/4.6
Use the link below to check your answers to Try This 1.
Possible TT1 (Try This 1) Solutions
--------------------------------------------------------------
 Tip
Tip
When writing answers for finding a missing angle, ALWAYS drop the words sin, cos or tan when writing the value of an angle and put the < sign in front.
DO write them as <A = 45o
DO NOT write them as sin A = 45o, cos A = 45o, or tan A = 45o
---------------------------------------------------------------
Now it is time to look at the process used to find a missing angle in a right triangle. Consider the triangle below: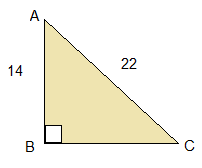
Find <C.
Start by identifying the given sides.
14 is the side opposite <C, 22 is the hypotenuse.
So using SOHCAHTOA, we have the OH and we need to write a sin statement.![]()
Now evaluate using the ![]() button.
button.
Calculator button sequence is:
2nd sin (14/22) enter
<C = 40o.
 Read
Read
Here is a chance for look through some more example to see how the sine, cosine, and tangent ratios are evaluated and used to determine angles. Pay careful attention to the difference between a trigonometric ratio and the angle that it can be used to find.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Carefully read through “Example 1: Determining the Tangent Ratios for Angles” on page 72 and “Example 2: Using the Tangent Ratio to Determine the Measure of an Angle” on pages 72 and 73. These examples will take you through the detailed steps of labelling your triangle and calculating unknown angles using the tangent ratio.
Now read two examples of the sine and cosine ratios. First, read “Example 1: Determining the Sine and Cosine of an Angle” on page 92. Next, turn to “Example 2: Using Sine or Cosine to Determine the Measure of an Angle” on page 93. The great thing is that if the labelling of the triangles makes sense, you will see that the sine and cosine ratios follow a similar pattern as the tangent ratio did.
 Did You Know?
Did You Know?
|
Although triangulation for map-making was used as long as 2500 years ago, it was also used as recently as the 1960s. Prior to the advent of the global positioning system (GPS) in 1973, one of the main techniques for determining distances in map-making was triangulation. For instance, triangulation was used to create an accurate map of Britain during the Principal Triangulation of Britain between 1783 and 1853 and again during the Retriangulation of Great Britain between 1936 and 1962.
In both cases, distances and angles were measured and trigonometry was used to fill in a detailed map of the country. |
 |
Example (from lesson 8)

© City of Edmonton. Used under Creative Common - Attribution-Noncommercial-Share Alike 2.5 Canada Licence
Using the same picture from Lesson 8, consider one of the triangles:
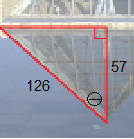
Find <Θ. Round to the nearest degree.
(Note: Θ is a greek letter said theta and is often used in trig)
In this triangle, 57 is the adjacent side to Θ and 126 is the hypotenuse.
So using SOHCAHTOA, we have the AH and we need to write a cos statement.![]()
Now evaluate using the ![]() button.
button.
Calculator button sequence is:
2nd cos (57/126) enter
Θ=63o
 Self-Check
Self-Check
Now that you have some experience with trigonometry, see how well you can answer the following questions.
SC 1. In the following triangle, what side is adjacent to <MLN? ** Note - this is another way to write <L. The middle letter is the angle you are looking for. So <L = <MLN**
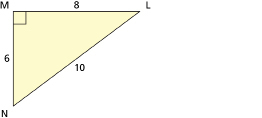
SC 2. Calculate the cosine of <MLN.
SC 3. Calculate the angle measurement of <MLN, to the nearest degree. Try to do this three different ways.
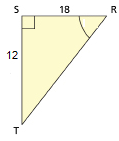
SC 4. Find the measure of <R, to the nearest degree.