Lesson 10: Solving Right Triangles and Word Problems
Created by IMSreader
Explore 2
Module 1: Measurement and Its Applications
 Did You Know?
Did You Know?
Trigonometry is used in the fields of design, music, navigation, cartography, manufacturing, physics, optics, projectile motion, and other disciplines that involve angles, fields, waves, harmonics, and vectors.
Trigonometry problems vary in complexity. Some problems involve only one right triangle and one or two steps. Other problems may involve two triangles and may require several calculations. You can approach these problems by following these guidelines:
- Sketch the scenario: Set up the problem with a drawing.
- Find the right triangle(s): You will need to identify the triangle or triangles in your sketch. Label the given lengths and/or angles. Also, label the length or the angle that you need to find.
- Write a trigonometric equation: Use SOH CAH TOA and the information given in the problem to select an equation—sine, cosine, or tangent—to solve.
- Solve the equation: Rearrange the equation, and solve for the unknown length or angle.
 Math Lab: Creating a Clinometer
Math Lab: Creating a Clinometer
Print the document Math Lab: Creating a Clinometer (or copy by hand) and complete the excercises. Some of this will be included in your Module Assignment.
Math Lab Analysis Answers
Example
Retrieve your data from Math Lab: Creating a Clinometer that you saved to your course folder ( binder). This example will take you through the steps that were just outlined to help you determine the height of the structure you measured.
One of the required measurements from the Math Lab is the angle of elevation from the horizontal to the top of the structure that you measured. Read the Caution bubble to see how to make sure you read the information correctly.
 Caution
Caution
man: © Robert Kneschke/shutterstock
Figure 1
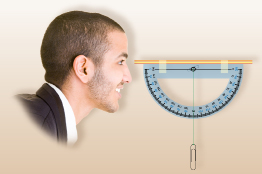
When the clinometer is held parallel to the ground along the horizontal, the string passes through 90° (see Figure 1).
Suppose that when the clinometer is tilted to view the top of the tree, the string now passes through 120° (see Figure 2).

man: © Robert Kneschke/shutterstock
Figure 2
The reading that should be reported is 120° − 90° = 30°.
This is because the clinometer started at 90° and then rotated through 30° to reach 120°.
If you recorded 120° as the angle of elevation, it means that you started at the horizontal and rotated your line of sight 120° upwards. Since a 90° rotation would mean you would be looking straight up, 120° would mean you are now looking slightly behind you.
For this example, assume that the measurements taken were the following:
- The distance between you and the base of the tree is 10 m.
- The string on the clinometer passes through 140°.
- The distance from the ground to the eye level of the person taking the measurement is 1.5 m.
Follow the steps to solve for the height of the tree.
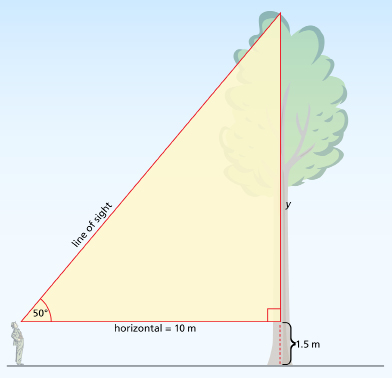
Sketch the Scenario
The angle of elevation is 140° − 90° or 50°.
A sketch might look like the following.
man, tree: Image Club ArtRoom/Getty Images
Find the Right Triangle(s)
The right triangle is coloured red. The distance between you and the tree is 10 m. The angle of elevation is 50°.
The length that needs to be found is y.
Write a Trigonometric Equation
Using 50° as the reference angle, the known side is the adjacent side, and the required side is the opposite side.
The ratio that contains both of these sides is tangent (TOA). So the equation is
![]()
Solve the Equation
Multiplying both sides of the equation by 10 gives the following:
![]()
Don’t forget to add the height to eye-level!
The height of the tree is 11.9 m + 1.5 m = 13.4 m.
 Try This 3
Try This 3
Apply the steps shown in the example to your own measurements to obtain the height of the structure you selected in Math Lab: Constructing a Clinometer.
Be sure to include the following:
- A description of the structure you chose.
- All of your measurements.
- All of your calculations, including sketches.
- A final answer along with an assessment of how reasonable it is.
Save your work as you will hand it in as part of your Module 1 Part 2 Assignment.
 Read
Read
You now have an idea of the approach you can take with trigonometry problems. Read the following examples to see how you can apply this same approach given different circumstances. Read the textbook that you are using for this course.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 3: Solving an Indirect Measurement Problem” on page 100 to see how to approach a similar problem where a measurement is made indirectly. Why can’t you use tangent to solve this problem?