Lesson 1: Factors and Multiples
Module 2: Roots and Powers
Prime Factorization
A number that is not a prime number and has a positive factor other than 1 or itself can be called a composite number. Composite numbers can be expressed as a product of prime numbers. This is called prime factorization.
Example 1
Express the number 60 as a product of prime numbers.
Solution
There are different ways of doing this that all lead to the same result.
The Prime Factorization applet demonstrates how you can use a factor tree to solve this problem. Use the applet to construct a factor tree to help you break 60 into its prime factors.
Depending on how you approached the problem in the example, your factor tree may look different from those of your peers.
Use the applet and the method of factor trees to express the number 144 as a product of primes. Save the factor tree to your course folder.
 Tips
Tips
The usual way of expressing a prime factorization is to write the primes from least to greatest. This way, you can see how many of each factor is required.
Practise your prime factorization skills without using a factor tree.
Play the Prime Number Shooter interactive game a few times and try to beat your own high score! (Make sure to read the instructions before playing).
You can use the prime factorization of a set of numbers to determine the greatest common factor of those numbers. The greatest common factor, or GCF, is the largest number that is a factor of all numbers in the set.
You can also use the prime factorization of a set of numbers to determine the lowest common multiple of those numbers. The lowest common multiple, or LCM, is the smallest number that is a multiple of all numbers in the set.
Example 2
Consider the numbers 48 and 60.
1. Find the GCF.
2. Find the LCM.
Solution
Use prime factorization to express 48 and 60 as products of primes.
48 = 2 × 2 × 2 × 2 × 3
60 = 2 × 2 × 3 × 5
- GCF
Step 1: Identify the factors that both numbers have in common.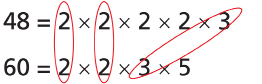
In this case, 48 and 60 have 2, 2, and 3 in common.
Step 2: Multiply the common factors together.
2 × 2 × 3 = 12
The greatest common factor is 12. - LCM
Step 1: Identify the factors that both numbers have in common.
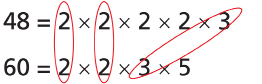
Step 2: Identify factors that are unique to each number. Circle these.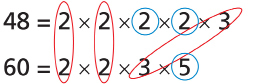
The common factors are 2, 2, and 3.
The unique factors are 2, 2, and 5.
Step 3: Multiply the common factors and unique factors together.
(2 × 2 × 3) × (2 × 2 × 5) = 240
The greatest common factor, or GCF, is the number that contains all the factors common to the numbers in the set. On the other hand, the least common multiple, or LCM, is the smallest number that contains all of the prime factors of each number in the set.
 Tips
Tips
As you practise prime factorization, you may be unsure of whether certain numbers are prime or not. In the Discover section of this lesson, you created a chart of all prime numbers under 100. By referring to this chart, you can check whether a number is prime.

