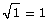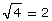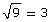Lesson 3: Irrational Numbers
Created by IMSreader
Module 2: Roots and Powers
Explore

© John R. Smith/shutterstock
Computer manufacturers have many ways of testing the strength of the computers they make. One way they do this is with software that enables a computer to evaluate the constant pi to a large number of decimal places. If the computer can correctly evaluate pi to a predetermined number of decimal places—usually in the millions—then it has shown that it can perform billions of calculations without an error.
Glossary Terms
Add the following terms to your "Glossary Terms" page:
- graphic organizer
- irrational number
- nested diagram
- rational number
-----------------------------------------------------------
Rational numbers are part of the real number system. Any number that can be written as a fraction is considered rational. More specifically, rational numbers can be expressed in the form 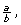 where a and b are integers
where a and b are integers 
 Caution
Caution
It is not possible to evaluate division by zero since the answer is undefined. You can think about it this way:
When you are asked to evaluate 6 ÷ 2, you must determine how many groups of 2 objects you must gather to have a total of 6 objects. The answer is 3 groups.
When you are asked to evaluate 24 ÷ 6, you must determine how many groups of 6 objects you must gather to have a total of 24 objects. The answer is 4 groups.
However, when you are asked to evaluate 2 ÷ 0, you must determine how many groups of 0 you must gather to have a total of 2 objects. In this case, it is impossible to gather enough groups of 0. No matter how many groups you gather, you will still have nothing. Therefore, division by 0 is considered undefined.
All integers are examples of rational numbers since any integer can be written as a fraction by adding a denominator of 1.
For example, both 10 and −10 are integers. These integers can be expressed as the fractions 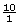 and
and 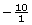 , respectively.
, respectively.
Decimals are rational numbers as long as their digits terminate or repeat. For example, the following decimals are rational:
6.12 −30.8924 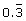
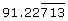
So what is an irrational number?
Irrational numbers include all those numbers that are not rational numbers. These are the numbers that cannot be written in the form 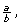 where a and b are integers
where a and b are integers 
Practically speaking, you can think of irrational numbers as decimals that neither terminate nor repeat.
For example, ∏ is 3.141 592 6 . . . . Even though ∏ has been calculated to over 1 trillion decimal places, a pattern in the digits has not been discovered.

Other examples of irrational numbers include the square root of certain numbers.
If the sides of the triangle are each equal to 1 as seen in the diagram, then according to the Pythagorean Theorem, 12 + 12 = 2, so that the hypotenuse is 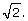 Since there is no rational number whose square is 2,
Since there is no rational number whose square is 2, 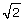 is therefore an irrational number.
is therefore an irrational number.
What about the square root of other natural numbers?
|
|
|
|
|
|
|
|
|
|
|
|
Do you notice which kinds of numbers in the table are rational and which ones are irrational?
The information in the table suggests that square roots of numbers that are not perfect squares are, in fact, irrational. One way to prove this statement is shown in the video clip titled “Root 2 Proof” in the Watch and Listen section.
 Caution
Caution
Since a calculator has a limited amount of space across its screen, it is not the best way to determine whether a number is irrational. For example, 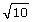 appears as 3.16227766 on some calculators. Since it appears to be a terminating decimal, you might incorrectly assume it is irrational. The best way to know whether the square root of a number is irrational is to figure out whether the number is a perfect square.
appears as 3.16227766 on some calculators. Since it appears to be a terminating decimal, you might incorrectly assume it is irrational. The best way to know whether the square root of a number is irrational is to figure out whether the number is a perfect square.