Lesson 3: Irrational Numbers

Module 2: Roots and Powers

 

Lesson Assessment

Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.  .

 

Project Connection **NOT ASSIGNED**

 

How do you create a cipher based on irrational numbers? Read the following introduction to substitution ciphers with shifts. Then examine an application of this cipher system using irrational numbers.

In cryptography, the term plaintext refers to the letters in the message, whereas the term ciphertext refers to the letters or numbers after the message has been encrypted. You have already seen what a substitution cipher looks like. Here is another version that does not use prime numbers. The following table is called a cipher strip.

In this case, the message “SECRET CODE” would be encrypted as follows:

18 4 2 17 4 19 2 14 3 4

This code would be easy to break as soon as you recognize that each number represents the position of each letter in the alphabet relative to A. So, the ciphertext that corresponds to the letter C is 2 because C is two letters away from A. You can make the code a little tougher to break by shifting the numbers along the bottom.

You can make the code a little tougher to break by shifting the numbers along the bottom.

Now the message “SECRET CODE” would be encrypted as follows:

19 5 3 18 5 20 3 15 4 5

Since a would-be code breaker would not know how the second row is shifted, the task of breaking the code becomes more difficult. To make the code even more difficult to break, you could introduce a different shift for every letter of the message. To do this, first create an extended cipher strip that includes at least ten possible shifts.

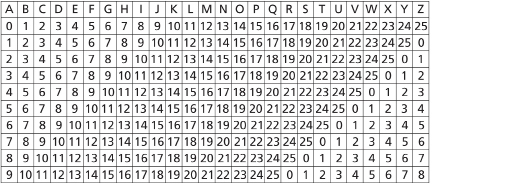
This table shows only ten shifts, but it could be extended for up to twenty-five different shifts.

You can use this block of data to create a cipher based on irrational numbers. The main feature of an irrational number is the fact that it presents an unending source of patternless digits. You can use this to your advantage when creating a cipher.

Follow these steps to encode a secret message:

Step 1: Choose an irrational number. This is the key.

Let be the key.

Step 2: List the digits of the irrational number beyond the decimal point:

So, the digits of beyond the decimal point are 141592653589793238 . . . .

Step 3: Write the digits below each of the letters in your message. You will only use as many digits as you need.

If you want to encode the message “SECRET CODE,” then write

Step 4: Use the number under each letter as the shift required to encode the letter.

• Since S has a shift of 1, it is encoded as 19. (Look at where the number 1 in the first column and E across the top row intersect.)
• Since E has a shift of 4, it is encoded as 8.
• Since C has a shift of 1, it is encoded as 3.
• Since R has a shift of 5, it is encoded as 22.
• Since E has a shift of 9, it is encoded as 13.
• And so on . . .

The completed cipher text is written as follows:

19 8 3 22 13 21 8 19 6 9

Notice that although there are two values of 19 in the cipher text, each one actually represents a different letter! Also notice that although there are three instances of the letter E in the message, each one is represented by a different number!

Reflect on these questions:

1. What are the steps for decoding a secret message using the cipher just explained? Use as the key to decode the ciphertext 3 4 5 23 9 19 into plaintext. (The result is the name of someone who was the first to use substitution ciphers with shifting.)
2. What are the benefits and drawbacks of this cipher?

At this time, go to the Unit 2 Project and complete the Module 2: Lesson 3 portion of the project.

 

Going Beyond

 

Phi, 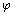, is an irrational number that is sometimes known as the golden ratio, the golden mean, and the divine proportion.

The value of phi (pronounced fee) is given the mathematical expression 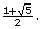The decimal equivalent of this expression begins with 1.618 03 . . . .

Although less celebrated than pi, phi is nevertheless a special number.

In Dan Brown’s book entitled The Da Vinci Code, professor Robert Langdon tells a class of university students:

Dan Brown. The Da Vinci Code Special Illustrated Edition. New York, Doubleday, 2003. p. 100.

Make a chart similar to the one that follows. Ask someone to help you measure the following lengths of your body. Then divide Measurement A by Measurement B in each row to obtain the ratio.

Measurement A	Measurement B	Ratio of Measurement
tip of head to floor	belly button to the floor
shoulder to fingertips	elbow to fingertips
hip to floor	knee to floor
fingertips to elbow	wrist to elbow

 

Answer the following questions:

1. Look at the ratios in the final column. How close are they to ?
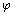2. Complete the chart of body measurements again by taking the measurements of a friend, classmate, or relative. How close are his or her results to ?
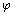3. Conduct an Internet search to find out what other aspects of the human body relate to 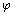. Use the search terms “golden section” and “divine proportion.” What other ratios did you find out are close to ?

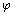Suggestions for further investigation:

• Borrow the book The Da Vinci Code by Dan Brown from your local library and read Chapter 20 to see what other examples Professor Langdon gives regarding the manifestation of 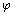in nature.
• Conduct an Internet search to see how 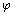was originally discovered. Use the search terms “phi,” “golden mean,” and “divine proportion.”

Mathematics 10C Learn EveryWare © 2010 Alberta Education