Math 10C Module 2 Lesson 3

Module 2: Roots and Powers

 

Lesson 3 Summary

A graphic organizer is a visual display that is used to depict the relationships between facts, terms, and/or ideas within a learning task. It forms a powerful visual picture of the information that allows the mind to discover patterns and relationships it otherwise may have missed.

 

Have you ever seen a set of Russian nested dolls like the ones in the photo? You open up the first one by separating the top half of the doll from the bottom half only to find a second doll nested inside. When you open up the second doll, you find a third doll inside. As this continues, the dolls become smaller and smaller until the smallest doll is found with the same proportions as the original. The real number system can be represented in this same nested fashion.

In Lesson 3 you investigated the following questions:

  • How are irrational numbers different from rational numbers?
  • How are the properties of irrational numbers suited to code construction and other applications?

You have learned that a rational number can always be written in the form 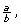where a and b are integers

In decimal form, a rational number is either terminating or repeating.

An irrational number cannot be expressed in the form 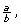where a and b are integers

A decimal number that does not terminate and does not repeat is called an irrational number.

While the rational numbers can be depicted as a nested diagram as shown, irrational numbers cannot be so depicted. A number cannot be both rational and irrational at the same time.

By virtue of their unending patternless digits, irrational numbers are well suited to code construction.

You learned how to locate irrational numbers on a number line using several methods. The first one used a calculator to evaluate the irrational number. The second method involved using benchmarks to approximate the location of an irrational number. The third method, less efficient, though more accurate than the others, was to use a compass and straightedge to place an irrational number on the number line precisely. You also practised sorting a set of numbers into rational and irrational numbers.

In the next lesson you will learn how to simplify radicals.

Â