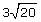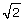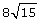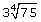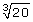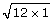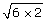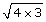Lesson 4: Mixed and Entire Radicals
Module 2: Roots and Powers
Explore
© moxduul/shutterstock
The word radical has both Latin and Greek origins. From Latin, it means “root” and in Greek it means “branch.” In Lesson 2 you discovered ways to calculate the square root of a perfect square and the cube root of a perfect cube. In this lesson you will learn how to work with the roots of numbers that are not perfect squares or perfect cubes.
Glossary Terms
Add the following suggested glossary terms:
- entire radical
- index
- mixed radical
- radical
- radicand
- root
--------------------------------------------------------
Recall your work with the volumes of cubes. If you know the volume of a cube is 27 cm3, then you can determine the length of one side by using the formula V = s3. Here, V is the volume of the cube and s is its side length.
V = s3
27 = s3
To obtain the answer, you would cube root both sides of the equation. (Again, you may want to use your Perfect Squares and Perfect Cubes Data Sheet you created in Lesson 2 and saved in your course folder.)
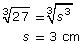
In this example you determined the cube root of 27 to find the side length of the cube. The expression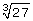 
is called a radical.
Study the diagram to understand how to name the parts of a radical.
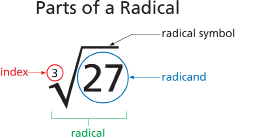
The radicand is the number or expression that appears underneath the radical symbol.
The index identifies the type of root. For example, a square root has an index of 2. A cube root has an index of 3. A fourth root has an index of 4, and so on.
Tips
In the case of square roots where the index is not shown, the index is assumed to be 2.
For example, the index for each of the following radicals is 2:
Sometimes a radical may have a coefficient, or a number in front of the radical symbol, separated from the radicand. A radical whose coefficient is a number other than 1 is called a mixed radical. On the other hand, a radical with a coefficient equal to 1 is called an entire radical. The following chart has examples of mixed radicals and entire radicals.
|
Mixed Radicals |
Entire Radicals |
|
|
|
|
|
|
|
|
|
Caution
There is a difference between 
and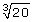
.
The radical 
means three times the square root of 20 and is approximately equal to 13.4164.
The radical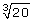 
means cube root of 20 and is approximately equal to 2.7144.
In Lesson 2 you learned how to find the square and cube roots of perfect squares and perfect cubes.
What if you are asked to find the square root of a non-perfect square such as 12? Well, you might say that 
is an irrational number. You could find a decimal approximation, but the only way to get an exact value is by simplifying the radical.
In the Discover section you found out the square root of the product of two numbers is equal to the product of the square roots of those numbers. This property can be summarized with the following expression:
where a and b are positive numbers
For instance, the expression 
can be evaluated as
.
The following example uses this concept to simplify
.
Example 1
Simplify .
Solution
The radical could be expressed as the product of square roots in several ways:
|
|
This is not helpful as it is exactly the same as the original radical, |
|
|
This expression simplifies to |
|
|
This expression is the most helpful one because it simplifies to |
but cannot be further reduced.
and since 
it can be further reduced to 
or just 
Sometimes, a radical is not a perfect square, but it may have a perfect square amongst its factors. To simplify the radical, you need to rewrite the radicand as a product of two factors, one of which is a perfect square. You can then simplify the square root of the perfect square and reduce the radicand. This process may need to be repeated until the radicand can no longer be reduced.
Example 2
Simplify the radical 
Solution
Method 1: Perfect Square Factors
or look for the largest perfect square and get
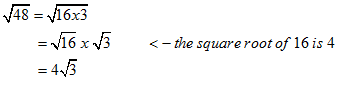
Method 2: Prime Factorization
Watch and Listen
Watch “Simplifying Radicals” that demonstrates the method by prime factorization.
Did you notice the result of simplifying an entire radical, 
is a mixed radical, 
Share
Compare your answers to the following questions with another classmate or appropriate partner ( if possible).
1. In Method 1, how can you avoid repeated factoring of the radicand?
2. In Method 2, how do pairs of identical factors become simplified? Can you show the math that makes this possible?
Record any similarities and differences you discussed in your course folder (binder).
Example 3
You can apply the same techniques to simplify radicals of different indices (plural form of index).
Solution
Method 1: Perfect Cube Factors
Method 2: Prime Factorization