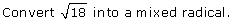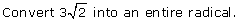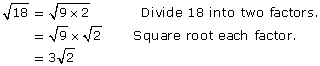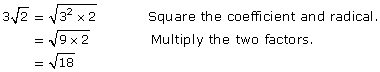Lesson 4: Mixed and Entire Radicals

Module 2: Roots and Powers

 Lesson 4 Summary

No one ever wants to be involved in a collision! Suppose you know the distance you need to stop your car, but can you stop it at the speed you are travelling? A very important application of radicals helps you find the maximum speed of a car to stop in a certain distance. The experimentation with objects in motion has shown that a relationship exists among the variables. For example, when you double your speed, your stopping distance quadruples.

Physicists have worked to create a formula that shows speed and stopping distance

	The variable S is the maximum speed.
	The variable a is the braking deceleration.
	The variable d is the distance.

In this radical expression, clear evidence is shown for why drivers should slow down in urban areas; a small reduction in speed leads to a much larger reduction in stopping distance. Solving the radical equation correctly here could quite literally save your, or someone else’s, life!

 

In Lesson 4 you investigated the following questions:

• How are mathematical processes reversed?
• How can the properties of radicals be used to simplify and order irrational numbers?

In this lesson you learned to identify the parts of a radical. You learned that an index of 2 means you can take one of two equal factors out from under the radical symbol. In a similar way, an index of 3 means you can take one of three equal factors out from under the radical symbol. By converting mixed radicals of the same index into entire radicals, you learned that you can compare the radicands to determine the correct sequence when ordering irrational numbers.

 

When you are encrypting a message, it is critical for you to be able to decrypt the code at a later time. Decryption is the reverse process of encryption. In a previous lesson you learned that you can reverse the single-step mathematical process of squaring by square rooting. Similarly, you can reverse the cubing of a number by evaluating the result’s cube root. In this lesson you examined another kind of mathematical process and its reverse process—converting between mixed radicals and entire radicals. Converting from an entire radical to a mixed radical is a two-step process. In the case of radicals with an index of 2, you first have to express the radicand as a product of two factors—a perfect square and a non-perfect square—and then you square root each factor. To reverse this you have to not only reverse each step but also in the reverse order.

 

Compare the following:

 

 

Notice that to convert to a mixed radical, you need to divide and then square root. On the other hand, to convert back to an entire radical, you need to square and then multiply. Therefore, each step is reversed, and the order of these steps is also reversed. The reversibility of processes is a recurring concept in mathematics. You will see this again in future courses when you examine inverse relations.

 

In the next lesson you will review the exponent laws. You will see by the last lesson of this module how radicals and exponents are related to each other. You will also learn how to convert between radicals and powers with rational exponents.

Mathematics 10C Learn EveryWare © 2010 Alberta Education