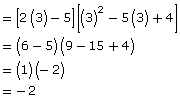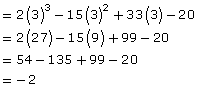Lesson 2: Multiplying Polynomials

Module 3: Polynomials

 

Explore

 

Nathan Sawaya is an artist who uses Lego building blocks as his medium. A former lawyer, Nathan is now making his childhood passion a full-time career.

 

Polynomials, such as binomials and trinomials, can be combined with other polynomials—much like toy building blocks can be combined with others of its kind.

 

Glossary Terms

 

 Add these terms and their definitions to your Glossary Terms page in your notes. You may also want to add examples that demonstrate how each term is applied.

• verify

--------------------------------------------------

In Lesson 1 of this module you learned to use the area method as well as the distributive property to find the products of binomials. You can apply those same methods to the multiplication of any two polynomials.

Example 1

Multiply (2x – 5)(x2 – 5x + 4) using each of the following two methods:

• area method
• distributive property

Solution: Area Method

Step 1: Set up a multiplication array with (2x – 5) along the left column and (x2 – 5x + 4) along the top row.

	x2	–5x	4
2x
–5

 Step 2: Complete the array.

	x2	–5x	4
2x	2x3	–10x2	8x
–5	–5x2	25x	–20

Step 3: Collect and combine like terms.

2x3 – 10x2 – 5x2 + 8x + 25x – 20 = 2x3 – 15x2 + 33x – 20

Solution: Distributive Property

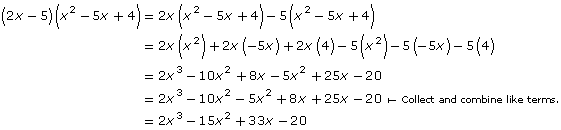
Retrieve your results from TT 1. You substituted a known value (x = 2) into the original multiplication expression. You discovered that the result was the same as when you substituted the same value into the expression representing the final product. The fact that the two results are equal makes sense since the two expressions are equal.

The following example shows how you can verify a product of two polynomials by using a two-column method.

Example 2

Verify the product in Example 1 by substituting x = 3.

Solution

• Create a chart divided into a left-hand column and a right-hand column.
• Substitute x = 3 in both expressions.
• See if the results are equal.

(2x - 5)(x2 - 5x + 4)	2x3 – 15x2+ 33x – 20

 Since both sides equal to the same value—in this case, –2—you have successfully verified the product expression to be correct when x = 3.

Self-Check

Take the opportunity to apply the concepts you have learned to these questions. Check your solutions afterwards.

SC 1. Multiply (3x – 5)(5x + 2) using the distributive property, and verify your answer.

SC 2. Multiply (y + 4)(y2 + 2y – 7) using the area method, and verify your answer.

Compare your answers.

 

Try This 6 - 7

 

Practice the methods you have learned for multiplying polynomials.

Complete the following in your course folder ( binder).

TEXTBOOK: Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 6. Complete “Exercises” questions 8 and 10 on page 186.

TT 7. a.   Choose at least two of the questions in TT 6 to verify. How do you select a value of x to use in verifying?

        b.   Are there values that are better suited for verifying than others?

Use the link below to check your answers to Try This 6 - 7

Possible TT6-7 (Try This 6 - 7) Solutions

-----------------------------------------------------------------

What happens if you verify a solution and you do not get results that are equal? In those cases, you may have committed an error either in your original multiplication or in the verification. In the remainder of this lesson, you will identify and explain common errors in solutions for polynomial multiplication.

Self-Check

 

For questions SC 3 and SC 4, you will be required to analyze a polynomial multiplication for errors. Try to identify the error and also explain how the expansion is carried out correctly. You may also wish to try to expand it on your own; then compare your solution with the given one.

SC 3. Michael expanded the following expression.

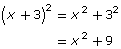
SC 4. Salma expanded the following expression.

Compare your answers.

 

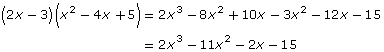
Try This 8

 

Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 8. a.   Complete “Exercises” question 13 on page 167.   

         b.   Complete “Exercises” questions 11 and 14 on page 186.

Use the link below to check your answers to Try This 8.

Possible TT8 (Try This 8) Solutions

Watch and Listen

Go the Khan Academy page linked below. You will find five questions to practice. If you have problems, there is a link to a video on the lower right corner.

 

Harder Multiplication questions

Example 3: Expand and simplify the following expression.

2( 3x - 1)( x + 2) - (x - 3) ( x + 4)

Solution 3:

Step 1: Start with doing FOIL on the first set of brackets and the last set of brackets.

2( 3x² + 6x - 1x - 2) - ( x² + 4x - 3x - 12)

Step 2: Collect the middle terms
2( 3x² + 5x - 2) - ( x² + x - 12)
Step 3: Multiply the 2 through the first bracket and the -1 through the second bracket. ** Note the subtraction sign is written as -1.

2( 3x² + 5x - 2) -1 ( x² + x - 12)

= 6x² + 10x - 4 - x² - x + 12  ** note the sign change in the last terms

Step 3: Collect like terms and finish
= 5x² + 9x + 8

Try This 9

 

Complete the following questions in your course folder ( binder).
Do all of the work and then use the link below to check your work.
a. -2( x - 5) (2x - 4) - ( 2x - 1)²

b. 3( 2a - 4b) ( 3a + 2b) + 5(4a- 1) ( 4a + 1)

Possible TT9 (Try This 9) Solutions

Mathematics 10C Learn EveryWare © 2010 Alberta Education