Lesson 2: Multiplying Polynomials

Module 3: Polynomials

 

Connect

 

Lesson Assessment

Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete. 

Project Connection **NOT ASSIGNED**

 

If you have ever watched a movie about espionage, you may have viewed a scene where two spies meet at a prearranged place to share classified information. Since the spies have never met before, they use secret passwords or phrases to ensure that they are sharing the information with the right person and not an enemy. This type of security measure is not limited to the realm of espionage; it is also evident in your day-to-day world.

 

A personal identification number, or a PIN, is often issued to you when you open a bank account or apply for a credit card. The PIN serves as a secret key to allow you to access secure information. In addition to this level of security, you are often also asked to provide an answer to a question that only you would know.

 

Examples of such questions might include the following:

• What is your mother’s maiden name?
• What is an important date for you?
• What was your favourite book as a child?
• What was the name of your first pet?

In the event that you lose your credit card or forget your PIN, you can still access information through a customer service agent. An agent will verify your address and birth date. This information, however, could be obtained by an unauthorized person. So in order to ensure that you are who you say you are, the agent will ask you to provide the answer to a predetermined question.

 

You can also use math concepts from this lesson to develop a similar security measure. Study the following example.

 

In this system, one person communicates a key word to the second person. The second person then communicates a number to the first person. The number that is communicated is based on an algorithm involving the letters of the key word.

 

In this algorithm, it will be important to know the position of each of the letters in the alphabet. Here is a table that can be used to identify letter positions.

 

 

Step 1: Assume the password is CARS. Write each letter in a table and its letter position according to the table above.

 

Letter	Position
C	3
A	1
R	18
S	19

 

Step 2: The first letter is a reference letter for the next two letters. In your box, subtract the position of the first letter from the positions of each of the second and third letters.

 

Letter	Position
C	3
A	1	1 – 3 = –2
R	18	18 – 3 = 15
S	19

 

Step 3: Place an x in front of each of these numbers to create two binomials.

 

Letter	Position
C	3
A	1	1 – 3 = –2	x – 2
R	18	18 – 3 = 15	x + 15
S	19

 

Step 4: Multiply the binomials together.

 

 

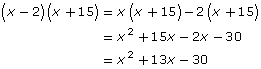
Step 5: Substitute the position of the last letter into the result from step 4.

 

 

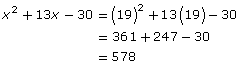
In this system, one person would communicate the key word to the other individual. The other individual would then perform the calculations in order to be able to respond with the correct number.

 

At this time, go to the Unit 2 Project and complete the Module 3: Lesson 2 portion of the project.

 

Going Beyond

 

In the Going Beyond section of Lesson 4 in Module 2, you investigated pencil-and-paper techniques for approximating square roots. One such method is by using a Taylor polynomial. Named for mathematician Brook Taylor, the Taylor polynomial can be used to approximate the square roots of numbers between 0 and 2.

 

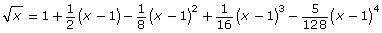
1. Evaluate the formula when x = 0.8.
2. What irrational number have you approximated?
3. Use your calculator to evaluate the irrational number. How does the calculator’s answer compare with what you obtained in question 1?

Use the Internet to further explore how other types of polynomials are used in math or real-world applications. You could also research what other mathematical contributions were made by Brook Taylor.

 

Mathematics 10C Learn EveryWare © 2010 Alberta Education