Lesson 3: Common Factors and Factoring Trinomials
Module 3: Polynomials
Connect
In this lesson you learned strategies that can be used to factor polynomials with common factors. You also learned how to factor a trinomial of the form x2 + bx + c. As you continue to learn new strategies for factoring different types of polynomials, you will want to keep track of these strategies in an organized fashion. Doing so will help you select the best method for factoring a given polynomial.
Open the Factoring Strategies document, and save (or copy it by hand). After each of lessons 3, 4 and 5 you can add to the document so that you have a summary of the different types of strategies for factoring and when to use which one.
![]() Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection ** NOT ASSIGNED**
Project Connection ** NOT ASSIGNED**
In Module 2 you learned about substitution ciphers where each letter of the alphabet is represented by a corresponding number. An Atbash cipher is a substitution cipher where each letter of the alphabet is represented by another letter. The table below shows the substitutions for an Atbash cipher.

Example
Translate the ciphertext MFNYVI using the Atbash cipher
Solution
Using the table, substitute the letter that appears above or below each letter in the ciphertext to obtain the plaintext. Use the table that follows. The ciphertext is shaded green. The plaintext is shaded yellow.
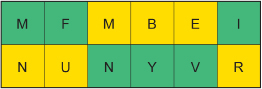
The plaintext is NUMBER.
The Atbash cipher can be rotated around like the tread on a treadmill. For example, you can shift it three positions clockwise. The resulting cipher looks like the following:

Notice that all 26 letters of the alphabet are still represented sequentially. The only difference is that A is not found at the beginning!
Example
Use the new version of the cipher to encrypt NUMBER.
Solution
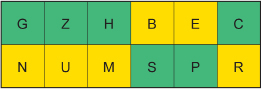
The ciphertext is GZHSPC.
You can create many variations of the same cipher just by rotating the original cipher clockwise any number of positions. In order for your message to be decoded properly, your recipient will need to know which variation of the cipher you used. You can do this by simply giving the recipient two letters that are in the same column. For example, you can give them G and N.
To add an additional level of security, you can encrypt those two letters as binomials. The following steps show a simple way to do this:
Step 1: Identify the position of each letter in the alphabet. Establish corresponding binomials.
|
Letter |
Position |
Binomial |
|
G |
7 |
x + 7 |
|
N |
14 |
x + 14 |
Step 2: Multiply the binomials to obtain a key for the encrypted message.
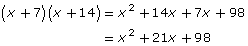
In this case, the sender would send the ciphertext along with the encrypted key. To decode the message, the recipient would have to
- factor the trinomial
- identify the letters represented by the binomials
- reconstruct the correct Atbash cipher variation based on those letters
- use the cipher to translate the message
Now go to the Unit 2 Project. Complete the Module 3: Lesson 3 portion of the project.
 Going Beyond
Going Beyond

© ZTS/shutterstock
Did you know that you can use your graphing calculator to verify that you have factored trinomials correctly?
To verify whether the factors are correct, follow the procedure:
Step 1: Enter the original polynomial into “Y1 =”.
Step 2: Enter the factored version into “Y2 =”.
Step 3: Execute the Graph command and observe carefully.
Step 4: If you see two distinct graphs, then the polynomial has been incorrectly factored. If the calculator graphs one graph on top of the other, then the polynomial has been graphed correctly.
Apply the above procedure to the following questions.
- Karim and Leona both factored x2 – 5x – 6.
Karim determined the factors to be (x – 2)(x – 3), whereas Leona determined the factors to be (x – 6)(x + 1).
Use a graphing calculator to verify their solutions. - Select two questions from your Lesson 3 Assignment where you were asked to factor a polynomial. Verify your solution using your graphing calculator.
In future math courses, you will learn more about how using a graphing calculator can not only help you to verify factoring but also to help you solve any equation.