Lesson 4: Factoring Trinomials of the Form ax^2 + bx + c

Factoring by grouping:

In order to explore the next strategy for factoring trinomials, you need to first consider the factoring of a four-term polynomial.
When factoring a four-term polynomial, you may notice that you can take a common factor out of some of the terms, but not all. If you put the terms into two groups, then you can sometimes take a common factor out of each group.
Example 2
Factor 6x² + 2y + 15x²y + 5y².

Solution
Step 1: Group the first pair and the last pair of terms.

(6x² + 2y) + (15x²y + 5y²)

Step 2: Take the greatest common factor out of each group. So factor a 2 out of the first two terms and factor a 5y out of the last two terms.

= 2(3x² + y) + 5y(3x² + y)

The key is to arrange the terms so that you have the same factors left in the brackets. See how, in the previous example, both brackets have the binomial (3x² + y).

Step 3: When the binomials are the same, the binomial is considered a common factor and you can divide it from each term in the expression.

         = (3x² + y)(2 + 5y)

So,
6x² + 2y + 15x²y + 5y² = (3x² + y)(2 + 5y)

Step 4: You can verify the result by multiplying the factors.

(3x² + y)(2 + 5y) = 3x²(2 + 5y) + y( 2 + 5y)
                         = 6x² + 15x²y + 2y + 5y²
( The order of the terms is different but it is the same polynomial expression)

Self-Check 2

SC 2. Apply the method of factoring by grouping to the following expressions.

1. x³ + x² + 4x + 4
2. 2ab + 2b² – 3a – 3b

Compare your answers.

Method 2: Factoring by Decomposition

** AGAIN - IT CANNOT BE STATED ENOUGH HOW IMPORTANT THIS SKILL IS FOR SUCCESS IN HIGH SCHOOL MATH**

Recall that multiplication and factoring are inverse operations. When you multiply two binomials, for instance, your result may be a trinomial. To recover those binomials, you can factor the trinomial.
In the Discover section of this lesson you investigated the multiplication of various binomials to discover a pattern for factoring trinomials of the form ax² + bx + c.

Retrieve the Math Lab: Factoring ax² + bx + c results that you completed in the Discover section. Look at the second row of your table.

It is also important to the discovery of a factoring technique that you notice another pattern. The leading coefficient and the constant (in the second and fifth columns) are equal to the product of the two x-terms (in the third and fourth columns). In other words, 2 × (–15) = –30 and 10 × (–3) = –30.

The factoring method of decomposition involves the breaking—or decomposing—of the middle term of a trinomial into two terms. Those terms must have a sum equal to the middle term of the trinomial. At the same time, the product of those terms must be equal to the product of the leading coefficient and the constant.
The decomposed polynomial can then be grouped and factored by common factors.

Example 3
Factor 2x² + 7x – 15 by decomposition.

Solution

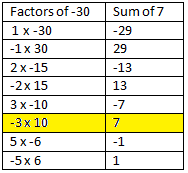
Step 1: Find two numbers whose product is equal to the product of 2 × (–15) and whose sum is equal to 7. Note this is DIFFERENT that trinomials we learned about in Lesson3. The product comes from the first term coefficient multiplied by the constant term.

Step 2: Use a product - sum table to list the factors and the sum of each set of factors.
Select the pair that can give you the same number as the middle term of the trinomial.

Step 3: Rewrite the trinomial as a four-term polynomial. Do this by breaking the middle term into the two terms found in the previous step.

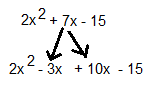
Step 4: Group the first two terms and the last two terms so that the expression is the sum of two binomials. ( This is grouping that you just practiced above).

= (2x² - 3x) + (10x – 15)

Step 5: Factor out the greatest common factor from each group of terms.

= x(2x - 3) + 5 (2x - 3)

Step 6: Factor out the common binomial.

=(2x-3) (x + 5)

Watch and Listen

For further explanation on the factoring strategy of decomposition, here are two videos to watch:

1.  Watch the video "Mathcast 011a - Using Algebraic Patterning to Factor a Trinomial "where he combines common factoring and factoring by grouping/decomposition in one question.

2. Watch a second video “Mathcast 11b Using Algebraic Patterning to Factor a Trinomial ‘Decomposition.’” This videos shows three skills: Finding the Product/Sum numbers, Common Factoring and then Factoring by Grouping/Decomposition.

Read

The following example demonstrates how a trinomial is factored by decomposition. As you read, look for the answers to these questions:

• What is the first thing you should do when you approach a factoring task?
• How can you systematically determine the numbers that meet the product-sum criteria?

Foundations and Pre-calculus Mathematics 10 (Pearson)
page 177 - 178 # 12, 13, 15, and 18.

Mathematics 10C Learn EveryWare © 2010 Alberta Education