Lesson 4: Factoring Trinomials of the Form ax^2 + bx + c: Explore 3

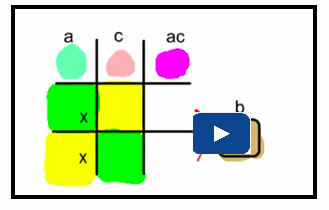
Method 3: Tic-Tac-Toe Method

You can also apply the concepts of decomposition using a graphic organizer to help you keep track of your work. This graphic organizer is a 3 × 3 multiplication array, similar to a tic-tac-toe square.

Example 4

Factor 3x² – 8x + 4.

Solution

Step 1: The first part is similar to decomposition. Find two numbers whose product is equal to the product of the first term times the third term or 3 × 4, or 12, and whose sum is equal to the middle term or –8.

Use a table to consider the possibilities. ** Think - since the product is positive and the sum is negative, BOTH numbers need to be negative.

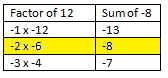
The numbers are –2 and –6, since the product is (–2) × (–6) = 12 and the sum is (–2) + (–6) = –8.

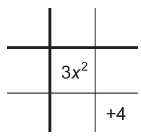
Step 2: Construct a 3 × 3 array as shown. Place the x²-term in the centre square. Place the constant in the last square in the bottom row.

This graphic shows a 3 × 3 array. The centre square reads 3x2. The bottom right square is +4.

Step 3: Place an x-term in the last square in the middle row and an x-term in the second square of the last row. These x-terms should have coefficients equal to the numbers determined in step 1.

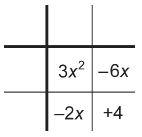
This graphic shows a 3 × 3 array. The centre square is 3x2. The bottom right square is +4. The square to the right of the centre square contains the term -6x. The square below the centre square contains the term –2x.

Step 4: Above each of the second and third columns, determine the GCF of the terms in the column. Ignore any negative signs for now.

3x² = 3 × x × x

2x = 2 × x

GCF = x

6x = 2 × 3 × x

4 = 2 × 2

GCF = 2

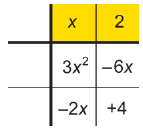
This graphic shows an array.

Step 5: Next to each of the second and third rows, determine the GCF of the terms in the row. Ignore any negative signs for now.

3x² = 3 × x × x

6x = 2 × 3 × x

GCF = 3x

2x = 2 × x

4 = 2 × 2

GCF = 2

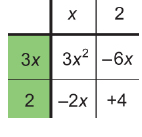
This graphic shows an array.

Step 6: Consider the signs of the terms in the top row and the left column. Remember that the product of two terms with the same sign is positive, while the product of two terms with opposite signs is negative.

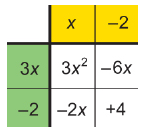
This graphic shows an array.

Since 3x² is positive, x and 3x can remain positive. On the other hand, if those terms are positive, then the 2 in the left column and the 2 in the top row must be negative in order to justify the –6x and –2x.

The factors are (x – 2) and (3x – 2).

Check by multiplying.

( x- 2) ( 3x - 2) = x ( 3x - 2) - 2( 3x - 2)

= 3x² - 2x - 6x + 4

= 3x² - 8x + 4

Watch and Listen

For further explanation on the tic-tac-toe method,

1. Go to this site that has several more problems solved.

2. Watch the video "Factoring Trinomials - Tic Tac Toe method"

Self-Check 3

SC 3. Practise using the method of decomposition or the tic-tac-toe variation of this method to factor the following.

2x² + 11x + 12
5x² - 7x + 2

Compare your answers.