Factoring Perfect Square Trinomials

Another type of special polynomial is the perfect square trinomial. A perfect square trinomial is the result of squaring a binomial.
Try the following exercise to see if you can uncover a pattern for factoring perfect square trinomials.

m10c_trythis.jpg Try This 2 - 8

Print (or copy by hand) and complete the following in your binder.

Try This 2 - 8 questions

Use the link below to check your answers to Try This 2 - 8.

Possible TT2 - 8 Solutions

Here is an example of how you can factor a perfect square trinomial.

 Example 4
Factor 9x2 + 12x + 4.


Solution
Step 1: Before you can apply a special strategy, you need to confirm that the trinomial is in fact a perfect square trinomial.
Are the first and last terms perfect squares?
Check:
9x2 = 3x × 3x
4 = 2 × 2
Both terms are perfect squares.
Is the middle term equal to twice the product of the square roots of the first and last terms?
Check:
2 × 3x × 2 = 12x
Yes, the middle term is twice the product of the square roots of the first and last terms.


Step 2: Write the trinomial as the product of two identical binomials whose terms are equal to the sum of the square roots of the first and last terms of the trinomial.
9x2 + 12x + 4 = (3x + 2)(3x + 2)
OR
9x2 + 12x + 4 = (3x + 2)2

What if you fail to recognize that a trinomial is a perfect square trinomial? Can a perfect square trinomial still be factored by the other methods that you have learned?

m10c_trythis.jpg Try This 9

Complete the following in your binder.

TT9: a. Factor 9x2 + 12x + 4 using at least two of the other trinomial factoring methods, such as algebra tiles, product-sum, decomposition, or inspection.


b. What conclusion do your results suggest? Do the results of factoring by other methods lead to the same answer?

Use the link below to check your answers to Try This 9.

Possible TT9 (Try This 9) Solutions

m10c_read.jpg Read

Read the following example to see how a perfect square trinomial can be factored by other methods. As you read, think about how you can modify your strategy of factoring perfect square trinomials so you can check the middle term at the end.

Foundations and Pre-calculus Mathematics 10 (Pearson)

Read “Example 1: Factoring a Perfect Square Trinomial” on page 190.

 m10c_trythis.jpg Try This 10

Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 10. Complete “Exercises” questions 4.c), 4.d), 8.a), 8.c), 8.f), 13.b), and 18 on pages 194 and 195.

Use the link below to check your answers to Try This 10.

Possible TT10 (Try This 10) Solutions

m10c_selfcheck.jpg Self-Check

As you practice factoring using the methods that you have learned in this lesson, you should be aware of some common errors that can occur. Some of these errors are due to inattention to details. Other types of errors reveal a misconception of the recently learned math principles.

The following Self-Check questions show how a student may factor a polynomial using the methods learned in this lesson.

SC 2. Study the solutions and identify the error that has been committed. Then correct the error and complete the solution.

1. Factor x4 – 16 completely.


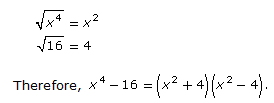
Since both x2 and 4 are perfect squares, this expression can be factored further.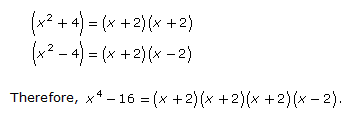

2. Factor 9x2 + 30x + 16.

Since both 9x2 and 16 are perfect squares, 9x2 + 30x + 16 is a perfect square trinomial.

Compare your answers.

 m10c_trythis.jpg Try This 11

Complete the following in your course folder ( binder). File them in your binder for future reference.
Practise troubleshooting factoring solutions. Be sure to identify the error and also correct it.

TT 11. Identify the error in each of these solutions. Then correct the error and complete the solution.

a.   Factor 4x2 – 4x + 1. Since both 4x2 and 1 are perfect squares, 4x2 – 4x + 1 is a perfect square trinomial.

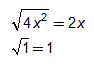
Therefore, the factored form is (2x + 1)2.   

b.   Factor (x2 – 5)2 – 16 completely. This is a difference of squares.


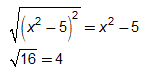
Therefore,

(x2 – 5)2 – 16 = ( x2 - 5 - 4)( x2 - 5 + 4)

                      = ( x2 - 9) ( x2 - 1)

Since both x2 and 9 are perfect squares:

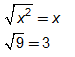
 (x2 – 5)2 – 16 = ( x2 - 5 - 4)( x2 - 5 + 4)

                      = ( x2 - 9) ( x2 - 1)
                      = ( x - 3) ( x + 3) ( x2 - 1)

Use the link below to check your answers to Try This 11.

Possible TT11 (Try This 11) Solutions

m10c_refcon.jpg Key Ideas

Part A

Return to your Factoring Strategies document. Update the document with the methods used in this lesson to factor differences of squares and perfect square trinomials. You should now have information in your chart about multiple types of factoring, including the following:

  • common factors

  • trinomial factoring

  • grouping

  • differences of squares

  • perfect square trinomials

With a partner ( if possible), compare the information that the two of you have included in your respective charts. Keep in mind that your chart is personal to you, so you may not have the same worked examples or tips about using a particular strategy. You may, however, notice some information in your partner’s chart that may be of benefit to you.

Reflect on these questions as you meet with your partner:

  • Am I missing any strategies that have been included on my partner’s chart but not mine? Should I include this information?

  • Are there any tips that I can pick up from my partner about a particular strategy?

  • Do I see any misconceptions in my partner’s chart? Does my partner’s chart reveal any misconceptions on my part?

  • Are my partner’s worked examples done correctly? Does my partner notice any errors in my examples?

Make any revisions you feel would improve your chart as a study tool and review document. You may wish to repeat this exercise with another partner.

 Part B


© Sideways Design/shutterstock

Another way you can represent the information you have added to the “Factoring Strategies” document is by using a flow chart. A flow chart can help you to visualize the steps required to factor a polynomial. The ability to visualize is especially helpful in cases where multiple steps are required before a polynomial is completely factored.

Using the information in your Factoring Strategies document, create a flow chart that helps you to decide when to use a certain factoring strategy.

To get an idea for how you can design this piece, go to the Internet and enter the keywords “Mathcast 015 Strategies for Solving Mixed Factoring Problems” in a search engine. This search should lead you to a video posted on YouTube. As you watch, try to identify what you need to know about a polynomial before you can select a factoring strategy.

You may also want to perform an Internet search using the keywords “factoring flow chart” or “factoring polynomials” and other related keywords to help guide you when you create your flow chart.
Put a copy of your flow chart in your binder.

You may use it along with your Factoring Strategies document to review key principles covered in this module.