Lesson 3: Functions

Module 4: General Relations

 

Explore

 

Did you know that the International Olympic Committee (IOC) recognizes 15 different disciplines in the Winter Olympics? Each discipline is comprised of several events. For example, figure skating has four events: men’s singles, ladies’ singles, pairs, and ice dance. Another example is the biathlon, which combines the disciplines of cross-country skiing and rifle shooting. At the 2010 Winter Olympics in Vancouver, the biathlon consisted of ten events. These events include individual, relay, sprint, and pursuit events in each the men’s division and the women’s division. While all of these events involve cross-country skiing and rifle shooting, only some are considered individual events, while other are considered team events.

 

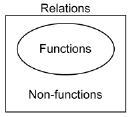
In this lesson you will learn about a special type of relation called a function. Functions are to relations what the individual events in biathlon are to the Olympic sport of biathlon. In other words, functions are a subset of relations.

 

 

Glossary Terms

Add the term function to your Glossary Terms section in your notes.

----------------------------------------------------------------------------------

Recall that relations are rules that connect one value to another. Relations can be described as ordered pairs in which the first value is the input and the second value is the output.

 

KEY IDEA A function is a relation where each input value corresponds to only one output value.

Try This 1

 

Retrieve the results of the Math Lab that you completed in the Discover section. Now that you have the definition of a function, complete the following.

TT 1. a.   Go back to your responses to the Analysis questions in Math Lab: Identifying Functions, and record reasons why each representation of the non-functions is not a function.      

        b.   Record reasons why the functions sets are functions.

Possible TT1 (Try This 1) Solutions

 

Read
Read the next example to see how you can identify an arrow diagram as a function and a non-function.

 

Example 1

 

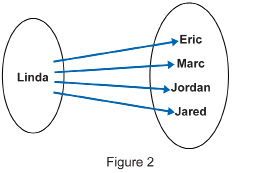
The Staal family from Thunder Bay, Ontario, is a famous hockey family. Henry and Linda Staal are the parents of sons Eric, Jordan, Marc, and Jared. Three of the four sons play professional hockey in the National Hockey League. The youngest, Jared, has been drafted and is taking steps to realize his dream of playing in the NHL.

 

Consider the two arrow diagrams representing the relationships in this family. (Note: The input is the name or names on the left-hand circle. The output is the name or names in the right-hand circle.)

 

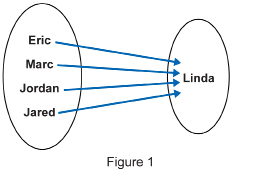
1. a. How is the input related to the output in Figure 1?
   
   b. How is the input related to the output in Figure 2?
2. Which arrow diagram fits the definition of a function? Why?

Solution

1. a. In Figure 1, each name on the left represents the son of the name of the person on the right.
   
   
   • Eric is the son of Linda.
   • Marc is the son of Linda.
   • Jordan is the son of Linda.
   • Jared is the son of Linda.
   b. In Figure 2, the name on the left represents the mother of each person named on the right.
   
   
   • Linda is the mother of Eric.
   • Linda is the mother of Marc.
   • Linda is the mother of Jordan.
   • Linda is the mother of Jared.
2. The arrow diagram in Figure 1 conforms to the definition of a function because each input value only has one output value. In this case, each son only has one mother. In Figure 2, the input value is associated with more than one output value. That is, Linda’s son is Eric and Marc and Jordan and Jared. This is still a relation, but it does not fit the definition of a function.
   
   Retrieve the results of the Math Lab you completed in the Discover section. You analyzed some relations represented by graphs, ordered pairs, and arrow diagrams. You formed a hypothesis about how to separate functions from non-functions.
   
   Now that you know what the definition of a function is, you can check your answers. The following example will revisit the three questions posed at the end of the Discover section, using different examples.

Example 2

 

For each pair of relations, decide which one is a function and which one is not a function. Explain your reasoning.

1. 
2. 
   
   
3. 

Solution 2

1. A function has only one output value for each input value.
   
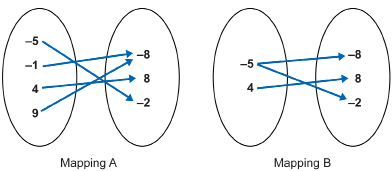
   In Mapping A, there is only one arrow leading out of each of the input values -5, -1, 4, and 9. (Even though there are two arrows arriving at the output value of -8, this does not contradict the definition of a function.) Therefore, Mapping A shows a relation that is a function.
   
   In Mapping B, there are two arrows leading out of the input value -5. This relation is not a function. Notice that even though there is only one arrow arriving at each of the output values -8, 8, and -2, this does not matter when identifying functions.
2. In Set A, the domain value of 2 is associated with two range values: 9 and -1. Therefore, Set A does not represent a function.
   
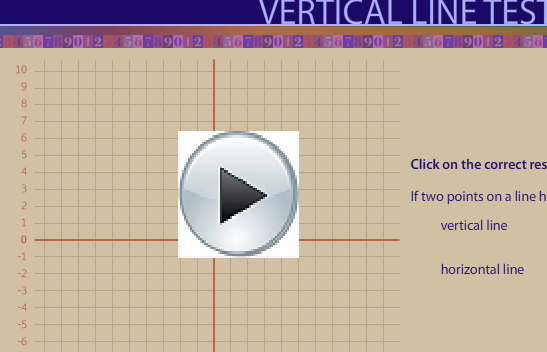
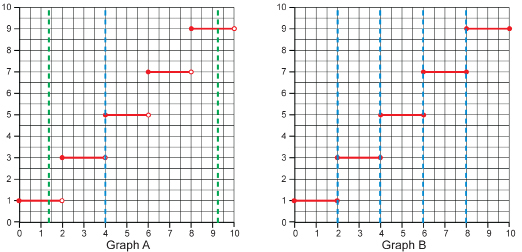
   In Set B, each domain value is associated with only one range value. Therefore, Set B is a function.
3. The graph of a function will not have any pair of points with the same x-coordinate. A test called the vertical line test can be used to quickly determine whether this is the case for a particular graph. Put a pencil or a ruler on your graph vertically. Keeping your pencil or ruler vertical, move it across the graph from left to right. If the vertical line simultaneously intersects the graph in two more points during any part of the movement or sweep, then the graph fails the test and is not a function. Otherwise, it is a function.
   
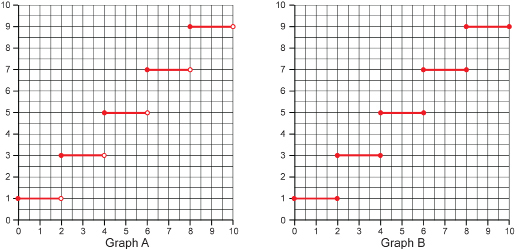
   Graph A passes the vertical line test since no two points line up along a vertical line. The following diagram shows several vertical lines drawn on the graph. The blue line seems to pass through two points, (4, 3) and (4, 5), but it does not. Since one of the points is open, it is not part of the graph. Therefore, there is only one value of the range associated with that value of the domain, namely (4, 5).
   
   Graph B fails the vertical line test in several places as shown in the diagram. In these places, there are two range values associated with the domain values 2, 4, 6, and 8.
   
   

Watch and Listen

 

View the “Vertical Line Test Demonstration” to see how the vertical line test is applied to both discrete and continuous graphs. See if you can determine whether each graph passes or fails the test before the line completes its sweep across the screen. Username is LA53 password is 4487.

---------------------------------

Here is another site that compares Relations and Functions.

----------------------------------

KEY IDEA The vertical line test is used to decide if a graph is a function or not. If a vertical line crosses the graph more than once in any location, it is NOT a function.

Read

 

Go to your textbook to study more examples of identifying functions. At the end of this section, you will be asked to describe your personal strategies for identifying functions based on how the relation is represented. As you work through the examples, you may want to write down some notes to help you remember your own strategies.

 

 

 

Try This 2

 

Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson)
TT2:  a.   Complete “Exercises” questions 4, 8, and 12 on pages 270 to 272.

        b.   Complete “Exercises” questions 5, 6, and 8 on page 294.

Use the link below to check your answers to Try This 2.

Possible TT2 (Try This 2) Solutions

 

Mathematics 10C Learn EveryWare © 2010 Alberta Education