Lesson 4: Slope
Slope of a Line Segment
 Try This 11 - 14
Try This 11 - 14
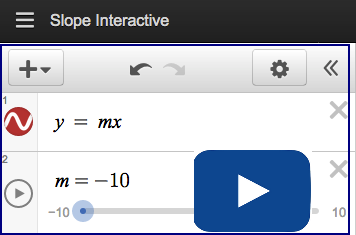
Use the Interactive Slope Applet to help answer the questions. You can drag the slider from -10 to positive 10 and watch what happens to the slope.
Keep your eye on the slope so you can see how it changes as you change the line.
As you explore with this applet, determine the following.
Complete these in your course folder ( binder).
TT 11. How are all line segments with positive slope similar?
TT 12. How are all line segments with negative slopes similar?
TT 13. a. What is the slope of a horizontal line segment?
b. Does the slope change as its length increases?
TT 14. a. What is the slope of a vertical line segment?
b. Does the slope change if the line segment is located in another part of the graph?
Use the link below to check your answers to Try This 11 - 14.
 Read
Read
Confirm your ideas about slope by reading your textbook. As you read, look for the reason why positive slopes are positive and negative slopes are negative.
|
Foundations and Pre-calculus Mathematics 10 (Pearson) Go to page 335, and read the bottom half of the page. Start reading where the vertical blue line shows along the page. |
How can you explain the values of the slopes of horizontal and vertical line segments?
Example 2
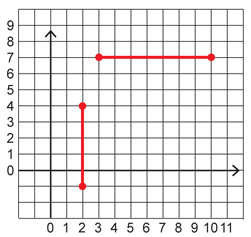
Using the diagram, determine the slope of the following:
- the horizontal line segment
- the vertical line segment
Solution
- In the graph of the horizontal line segment, the rise is zero units and the run is 6 units.
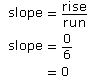
All horizontal line segments are flat and have a rise of zero. Since zero divided by any other number (besides zero) is zero, the slope of any horizontal line segment is zero. - In the graph of the vertical line segment, the rise is 5 units and the run is zero.

All vertical line segments have a run of zero. Since any number divided by zero is undefined, the slope of any vertical line segment is undefined.
 Print
Print
Print the following page for a summary of lines and their slopes.
Here is a fun way to remember slope - can you figure out what everything means on Mr. Slope guy?
Retrieve your Math Lab results. In the Discover section of this lesson, you investigated the steepness of a staircase. Since you were evaluating the rise divided by the run of a step, you now know that you were actually evaluating the step’s slope.
You may have noticed that the slope of a single step is equal to the slope of the entire staircase. Also, you may have discovered that the slope of one step is equal to the slope of any number of consecutive steps. This makes sense since a staircase is much safer if the steps are consistently steep.
Have you ever walked on stairs with steps that were not of consistent steepness? Or perhaps you have stepped onto or off of an escalator? What are the hazards of steps of varying slopes?
Just as the slope of a staircase can be determined by using any two steps along the staircase, the slope of a line or any segment of a line can be determined by knowing the location of any two points along the line or segment.
 Watch and Listen
Watch and Listen
There is a formula that you can use to determine the slope of any line, as long as you know the coordinates of two points on the line. Watch the “Slope of a Line” video to find out how to derive this formula. **Scroll down to find the video**
For this video, you will only need to watch certain segments. Watch from the beginning to the 1:05 minute mark. Then watch the section from 1:45 minutes to 4:05 minutes. As you watch these video segments, try to determine how the points are named.
When you know two points with coordinates (x1, y1) and (x2, y2), you can determine its slope, m, by using the following formula:
![]()
 Read
Read
Go to your textbook to see another example of how the slope formula is used. As you work through the example, think of those instances in which it may be more practical to use the formula than to use the rise over run method.
Foundations and Pre-calculus Mathematics 10 (Pearson)Read “Example 3: Determining Slope Given Two Points on a Line” on page 337. |
 Self-Check
Self-Check
SC 2. Use the slope formula to evaluate the slope of the line that passes through each pair of points.
- A(1, 3) and B(4, 9)
- C(−5, 12) and D(11, 6)
 Try This 15
Try This 15
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 15. Complete “Exercises” questions 4, 5, 6, 13, and 16 on pages 339 to 341. Note: For question 13, use the slope formula.
Use the link below to check your answers to Try This 15.
Possible TT15 (Try This 15) Solutions
Mathematics 10C Learn EveryWare © 2010 Alberta Education