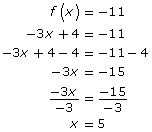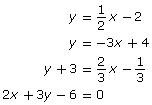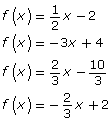Lesson 1: Function Notation
Module 6: Linear Equations
Explore

iStockphoto/Thinkstock
Some people enjoy songwriting or music composition as a way to spend leisure time. If you have a talent for writing lyrics or composing tunes, this can be a rewarding pursuit. It’s really easy to record your composition using computer software that simulates any number of instruments.
There is a special way to write music. The notation that is used in music involves symbols representing notes. A particular symbol reveals many things about how the note is to sound. For example, the position of the note indicates the pitch of the sound. The appearance of the note may reveal that the sound should be sustained for a long time or played rapidly in succession with another note. Notation in musical composition also tells you the rhythm of the piece and which set of notes will be used.
Have you ever watched musicians play music while reading the notes off of a sheet? That they can do it smoothly is a reflection of the fact that the system of notation for music is efficient. Similarly, in mathematics, functions can be represented in function notation. This type of notation emphasizes the input-output nature of functions and can be an efficient way of evaluating functions and reporting particular values on the graph of a function.
In this lesson you will write functions in another way—using function notation.
Glossary Terms
Add this term and its definitions to the Glossary Terms section in your notes. You may also want to add examples that demonstrate the term as well
-
function notation
---------------------------------------------------------------------------------------------------------------
Standard Notation vs Function Notation
Examine the following chart comparing equations expressed in standard notation and in function notation. Four different linear equations are shown in the left-hand column. The right column shows the same equations expressed using function notation. Compare the two columns and identify the key difference.
|
Standard Notation |
Function Notation |
|
|
|
You may have noticed that the key difference is that in function notation, f(x) replaces y. You may have also noticed that in function notation, the f(x) is always isolated. For instance, it is not appropriate to express a function as ![]()
 Try This 9 - 12
Try This 9 - 12
Use what you have discovered about the relationship between standard notation and function notation to complete the following questions below.
Complete the following in your binder.
TT 9. Express the equation of each linear function using function notation.
a. y = x + 1
b. x + 4y + 8 =0
TT 10. Express each equation in function notation as a linear function in two variables. The form of standard notation is indicated in each case.
a. f(x) = -3/4x + 1 ( Slope-intercept form)
b. f(x) = 2x -9 (general form)
Possible TT9-10 SolutionsUnlike standard notation, function notation gives names to functions. Usually, f(x) is used to represent the dependent variable when the situation does not indicate a particular context. The notation also shows the input value and the process by which the input is turned into a single output value.
The next example asks questions relating to a linear function as expressed using function notation. See if you can answer these questions before reading the solutions.
 Tips
Tips
Function notation is used to describe functions only. Relations that are not functions should not be represented with function notation.
Example
Consider the function given as f(x) = −3x + 4.
- What is the name of the function?
- How do you say the expression? What does it mean?
- Determine f(2).
- Determine the value of x when f(x) = −11.
Solution
- The name given to the function is f. Similarly, the name of the function g(x) = x is g and the name of the function h(x) = x2 + 4 is h.
- The expression can be read in different ways:
- f at x is equal to −3x + 4
- f of x is equal to −3x + 4
- f as a function of x is −3x + 4
- The expression f(2) means the “output of the function f when the input value is 2.” Note that in f(2), x has been replaced with 2. Therefore, you can make the same substitution on the right side of the equation.
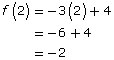
- The expression f(x) = −11 means that the output is −11. Your task is to find the value of x, or the input, under this condition. Here, you can replace f(x) with −3x + 4.