Lesson 1: Function Notation
Module 6: Linear Equations
Self-Check
After working through the Example problems, test your level of understanding by answering the following questions.
SC 1. If f(x) = 5x + 2, what is f(2)?
SC 2. If g(x) = −3x, what is g(−2)?
SC 3. If f(x) = −2x + 3, what is f(3)?
SC 4. If g(x) = −3x, what is x if g(x) = −18?
SC 5. If f(x) = 5x + 2, what is x if f(x) = −13?
SC 6. If g(x) = −2x + 3, what is x if g(x) = −2?
Recall that a function is a relation where each “input” value only has a single “output” value. Other input values may have identical output values as this function, but the important idea is that each input has only one output value.
Generally speaking, function notation is represented in this way:
f(input value) = output value
Another way of saying this is f(domain) = range.
The following is the graph of 
. Remember that this is equivalent to 
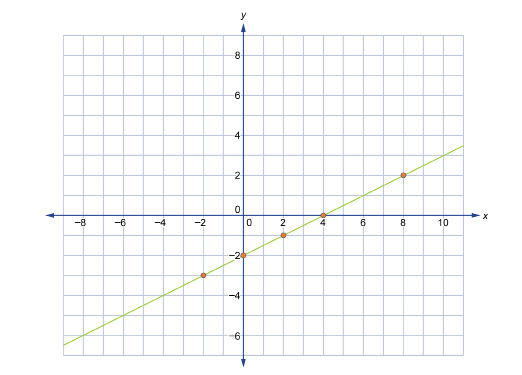
Recall that the line represents the linear function. Each point on the line is an ordered pair that satisfies the equation of the line. On this graph, the point (8, 2) has an x-coordinate of 8 and a y-coordinate of 2. In function notation, this relationship is expressed as f(8) = 2.
Try This 11 - 13
Complete the following in your binder.
Use the link below to check your answers to Try This 11 - 13.
---------------------------------------------------------------------
The symbol most commonly used to denote a function is f because function starts with f, but you may use other letters to express a function.
Consider the following example.
The formula for the circumference of a circle is 
Circumference is a function of the diameter. So, to express the formula in function notation you may want to use the letter C instead of f.
The formula expressed in function notation is 
Read this as “C as a function of d is 
” or “C of d is 
”
Think
Can you think of other formulas that could be expressed in function notation?
Read
Function notation is useful when applied to word problems. When this happens, you will see that the letter assigned to the function may not be f and will likely be a letter that is more suited to the variable it represents.
You will now work through an example in your textbook to see how function notation is used to determine values in a given context. As you do so, focus on two questions:
- How are letters chosen to represent both the independent and the dependent variables?
- How do you know whether you are supposed to evaluate the independent variable or the dependent variable?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 3: Using Function Notation to Determine Values” on pages 269 and 270.
Graphing a function expressed in function notation is identical to graphing the same function expressed in standard notation.
Try This 14
Print (or copy by hand) and complete the following in your binder.
Try This 14 Questions
Use the link below to check your answers to Try This 14.
Possible TT14 (Try This 14) Solutions
--------------------------------------------------
Read
Go to your textbook to see how you can sketch a linear function expressed in function notation. Compare the strategy used in the textbook with the strategy you used in TT 14.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Sketching a Graph of a Linear Function in Function Notation” on page 315.
The example shows how you can determine two points on the graph. What is special about these two points? How is function notation used to determine these points? What other strategies could you use to sketch the graph?
Self-Check
In this lesson you have learned how to interpret, express, and use linear equations written in function notation. Revisit the questions posed in TT 4 to TT 8 earlier in the lesson.
SC 7. Go to “Module 6: Lesson 1: SC 7.” Match TT 4 to TT 8 to the equivalent questions expressed in function notation.
-------------------------------------
Watch and Listen
Before finishing the lesson with some practice, watch this helpful video on Function notation. Note that on the left side of the screen, there are links to the practice questions and on the right, there are links to other sites.
--------------------------
Try This 15
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 15. a. Complete “Exercises” questions 6.a), 6.c), 7.b), 7.c), 14.a), 14.d), 15.b), and 19 on pages 271 and 272.
b. Complete “Exercises” question 16 on page 296.
c. Complete “Exercises” questions 6.a) and 15.a) on pages 319 to 322.
--------------------------------------------------
Watch the following video titled “What Is Function Notation?” This video summarizes the key points of this lesson. You will see how function notation is both interpreted and applied. ** You may need to click above the words in the white space to activate the video**
