Lesson 2: The Equation of a Line
Module 6: Linear Equations
Explore
© Galyna Andrushko/1472722/Fotolia
Mountaineering is a recreational pursuit that takes physical endurance and determination. Just as you can experience sicknesses due to rapid pressure changes in the depths of the ocean, you can also become sick at high altitudes. Altitude sickness, also called acute mountain sickness (AMS), is a condition that affects individuals whose bodies cannot take in enough oxygen at high altitudes. This condition occurs when the person does not allow time for his or her body to acclimatize to the diminished levels of oxygen at higher elevations. Experienced mountaineers will adopt a “two steps forward, one step back” approach to climbing. In other words, during the day the mountaineer will climb to higher elevations to push his or her bodies to adapt, but then at night the mountaineer will climb back down to base camp to sleep. Subsequently, the mountaineer will progressively climb to a higher elevation and then climb back down to a slightly higher base camp than the previous one.
Another effect of higher altitudes is that the boiling point of water is reduced. In fact, the relationship between the altitude and the boiling point is linear. For example, the normal boiling temperature of water is 100°C, but at 4000 m elevation, that critical temperature is closer to 86°C. So the next time you go mountain climbing, you can expect to eat your morning oatmeal a little sooner because you won’t be waiting as long for the water to boil!
Did You Know?
The higher the temperature, the faster food cooks. Even though water boils sooner at higher altitudes, food actually takes longer to cook! This is because the temperature of the boiling water is lower.
Glossary Terms
Add this term and its definitions to the Glossary Terms in your notes. You may also want to add examples that demonstrate how each term is applied.
-
linear equation
-----------------------------------------------------------------------
The approach to the determination of the equation of a line depends on the information that is provided. The equation of a line can be determined as long as you have two pieces of information: the slope and a point on the graph.
Recall from Lessons 3 and 4 of Module 5 that there are three forms for the equation of a linear function:
-
slope-intercept form
-
slope-point form
-
general form
You will find that the first two forms in the list are more practical to use when determining the equation of a line. However, you can still convert an equation written in slope-intercept or slope-point form into general form.
Generally speaking, when you are asked to write the equation of a line, you will be given either of the following:
-
the slope of the line and the coordinates of a point on the line
-
two coordinates points on the line
You have previously learned how to write the equation of a line in the form y = mx + b when you are given the slope, m, and the y-intercept, b.
In this lesson you will investigate how to write the equation of a line when given different information about the line.
-------------------------------------------------
Determining the Equation of a Line: Given Slope and Point
There are ways to write a linear equation when given its slope and a point on the line. This following video clip shows one method, and the example after the video clip shows an alternate method.
Watch and Listen
View the video titled “Linear Equation Given Slope and One Point.” Watch for the two equivalent versions of the equation at the end of the video. Can you convert the original equation into those two forms?
-----------------------------------
Consider another approach to finding the equation of a line when given the line’s slope and a point on the line. This approach is a graphical one. The next example shows how you can determine the equation of the same line that was presented in the video. As you work through the solution, see if you can detect both advantages and disadvantages in the method.
Example
Use a graphical approach to determine the equation of the line with a slope of 
that passes through the point (12, 8).
Solution
Plot the point (12, 8). Apply the slope of 
by rising up 1 unit and moving 4 units to the right. The second point will be plotted at (16, 9). Optional: You can get a third point by applying the slope of 
in a different way. You do this by dropping 1 unit and moving 4 units to the left of (12, 8). The new point will be located at (8, 7).
Join the points with a line.
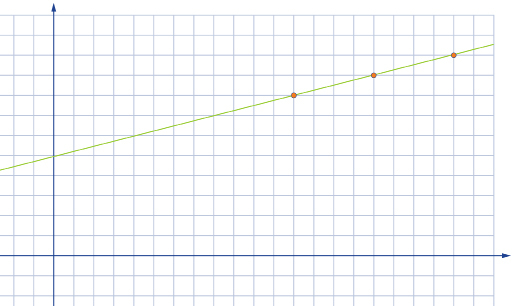
From the graph, you can see that the y-intercept is (0, 5). Since the slope is 
and the y-intercept is b = 5, the equation is 
Share 1 - 3
Review your answers to the Math Lab. Working with a partner ( if possible), respond to the following questions.
1. a. How is your approach similar to and different from the one presented in the example provided in the lesson?
b. How is your approach different from the one presented in the example provided in the lesson?
2. What advantages does a graphical approach have to finding an equation?
3. a. What drawbacks are there in using a graphical approach?
b. Does the use of a graph to determine the equation of a line work in all instances?
Read
Go to your textbook to work through an example that shows how you can write the equation of a line when given the slope and a point on the line.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Writing an Equation Using a Point on the Line and Its Slope” on page 368.
Not all equations are going to have integral coefficients. Some, as in this example, may have rational coefficients. Study carefully how the y-intercept, which is a fraction, is determined.
Self-Check
SC 1. Find the equation of a line, given m = −2 and the y-intercept = 4.
SC 2. Find the equation of a line in slope-intercept form, given that the slope is −3 and the line passes through (4, 6).
SC 3. If given slope 
and coordinates C(2, 6), what is the equation of this line in slope-intercept form?
SC 4. Find the equation of the line of slope 
and the y-intercept (0, 3).
Try This 1
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete “Exercises” question 5 on page 372. Write the equation in slope-point form; then convert to slope-intercept form and general form.
Use the link below to check your answers to Try This 1.
Possible TT1 Solutions