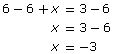Lesson 4: Applications of Linear Equations
Module 6: Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
Watch the video titled “Graphic Representations.” The video shows an example of how you can interpret the independent and dependent variables in a given context. As you watch, focus on where the independent variable and dependent variable are placed on a graph. You have viewed this video clip when you worked on Module 4.
-----------------------------
To review slope as a rate of change, you may want to revisit the work that you did in Module 4: Lesson 5. Work through the last Watch Sal Khan work through a number of examples on “Slope as a Rate of Change.”
---------------------------------------
Watch this helpful video on Function notation. Note that on the left side of the screen, there are links to the practice questions and on the right, there are links to other sites.
---------------------------------------
The basic rule used in solving equations in algebra is to balance both sides of the equation. In other words, what is done to one side of the equation must be done to the other side of the equation as well. For example, if you add a term on the left side, you must add the same term on the right side. If you multiply a term on the left side, you must multiply the same term on the right side. The following table shows how you can solve two different linear equations.
|
Solving a Basic Equation |
Solving by Combining Like Terms |
|
In the equation 6 = 3 − x, you want to get the x on the left side and the other items on the right side.
First, add x to both sides of the equation.
6 + x = 3 − x + x 6 + x = 3
Next, subtract 6 from both sides of the equation.
By following these two steps, you learn that x = −3, which is the solution to the equation. |
Consider the equation 2x + 3 = −4x − 7.
You can solve the equation by first getting all the x terms on the left side.
Add 4x to both sides.
2x + 4x + 3 = −4x + 4x − 7
Combine like terms.
6x + 3 = −7
Subtract 3 from both sides.
6x + 3 − 3 = −7 − 3
Combine like terms.
6x = −10
Divide both sides by 6.
Simplify the fraction.
|
Try the “Algebra Four!” equations game to practise your equation solving skills. ou can choose different types of questions to practise. Select “Two-Step Problems” and then play one round. Next, you can add “Variable on Both Sides” the second time you play. This game is best played with two people, so you may want to invite a classmate to play with you or perhaps your teacher or a parent may be willing to play with you. If you feel up to the challenge, you can select the first, second, and fourth options. (Do not select the “Quadratic” option as you will be learning how to solve quadratic equations in a future course.) As a warning, if you try the game, you may need to have a piece of paper and a pencil handy!
-----------------------------
Materials
You will need the following items in order to complete Math Lab: Counting Beats.
- CD or MP3 player
- music CD or MP3 song
- stopwatch or timepiece