Lesson 4: Applications of Linear Equations

Module 6: Linear Equations

Explore

 

A smartphone is a device that serves multiple functions. Many smartphones are not only cellphones but are also personal organizers, cameras, voice recorders, and portable media players with the ability to access the Internet. Used largely by those in the business world initially, smartphones have gained popularity with many people on the go. These devices offer its users GPS navigation, instant weather reports, e-readers, games, restaurant reviews, stock reports, and other applications.

Smartphones offer many conveniences, but they are not free. There is an initial fee and a subsequent monthly fee, depending on the plan that is purchased. The initial fee covers the cost of the device and varies depending on the length of the contract. The monthly fee depends on the options that are selected and the amount of time spent using the device. For example, you may be charged for how long you spend using the smartphone to surf the Internet. The cost of using a smartphone can be modelled by a linear function.

In this lesson you will model and solve problems using linear equations.

Glossary Terms

Add these terms and their definitions to your Glossary Terms section in your noted. You may also want to add examples that demonstrate how each term is applied.

• fixed term
• variable term

-----------------------------------

You already know that the equation of a linear function can be expressed as y = mx + b. This equation can also be expressed in function notation as f(x) = mx + b. When solving problems, you may want to choose meaningful letters to represent the independent and the dependent variables. For example, a distance-time problem could be represented by the letters d and t.

Try This 1 - 3

Complete the following in your binder.
TT 1, TT 2, and TT 3 provide descriptions of linear scenarios.
Identify the independent and the dependent variables, and select appropriate letters to represent them. Note: If you are still unsure about the terms independent and dependent, review the “Graphic Representations” video from the Refresher section of this lesson.

TT 1. As the cellphone usage increases, the cost also increases.

TT 2. A scuba diver swims in the depths of the ocean. The deeper she swims, the stronger the water pressure that is exerted on her body.

TT 3. A mountaineer climbs a very high mountain. The temperature drops with every kilometre he climbs.
Possible TT1-3 Solutions

Read

The linear problems that you will encounter will require you to do several things in sequence. Go to your textbook to look at the structure of different problems. Your focus is on what is being asked, not on the solutions. As you read, take note of what each part of the question requires. 

It is important to understand how problems are structured so that you know how to approach them. Look back at the structure of the Math Lab. Compare the order of the questions posed in the Math Lab and the same structure in the examples you have just read about in your textbook. Do you notice similar patterns? Why are the questions asked in that particular order?

Try This 4 - 8

Complete the following in your binder.
You may need to go back to your textbook and review the examples you have just read to answer these questions.

TT 4. Are there similarities between what is required by the first textbook example and the second textbook example?

TT 5. What key phrase is common among the questions that are posed in the textbook examples?

TT 6. a. How are the questions structured?

         b.   In what order are the parts arranged?         

TT 7. Why is the order of the parts important?

TT 8. What skills that you have previously learned will you need to recall or apply to answer each question?
Possible TT4 - 8 Solutions

Watch and Listen

Watch the video “Write a Linear Given Fixed and Variable Costs”  to get an idea for how to assign meaningful letters to variables and to learn how to solve a problem one part at a time. As you work through the lesson, pay attention to how the answer from each part is used to solve the next part of the problem.

-----------------------------

Here is a second example, showing the steps clearly as well.

-----------------------------

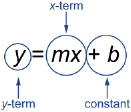
Analyzing the Parts of a Linear Equation

The slope-intercept form of a linear equation has three distinct parts as represented in the diagram shown.

Try This 9-11

© fokinol/11851192/Fotolia

Complete the following in your binder.
Try This 9 - 11 Questions
Use the link below to check your answers to Try This 9-11.
Possible TT9-11 Solutions

 

The x-term in a linear equation is known as the variable term since it varies according to the independent variable. The constant is known as the fixed term since it remains the same regardless of the value of the independent variable.

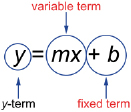
You can use the idea of the variable and fixed terms to translate descriptions of linear relations into equations. The part of the context that is constant—such as the CD wallet without CDs—is the fixed term. The part of the context that changes depending on the independent variable—such as the total mass of the CDs, which changes depending on the number of CDs—is the variable term.

Self-Check 1 - 4

Test your ability to identify the fixed and variable terms in the description of a linear situation. Also, see how accurately you can determine a correct linear equation for a given situation. Choose meaningful letters for the variables.

SC 1. Mominah works at an electronics store. She is paid a base salary of $1500 per month. She also receives a 6% commission on her monthly sales. Write an equation relating Mominah’s sales and earnings for one month.

SC 2. A cellphone plan charges the customer $30 per month plus $0.25 per text message. Write an equation relating the number of text messages and the cost of the plan for one month.

SC 3. Madelyn enters a piano festival in which there are numerous categories. Each category takes 40 minutes to complete. At the end of the festival, there is a 90-minute concert for all competitors. Write an equation relating the amount of time Madelyn spends at the piano festival and the number of categories she enters.

SC 4. The temperature at a base camp is 4°C. For every 1000 m elevation, the temperature drops by 6.5°C. Write an equation relating the elevation to the temperature.

Compare your answers.

Read

By working through the Math Lab and by reading in your textbook, you may have observed that problems are easier to tackle when broken into separate parts. These parts may include the following:

• identifying and assigning variables

• sketching a graph

• constructing an equation

• using the equation to predict other values

Sometimes the questions you encounter will guide you through each part, and, at other times, you will have to decide how to structure your approach.

You will now return to the examples that you have previously read. This time, focus on the solutions. Specifically, try to discover what information is important to each part of the question and how the information that is generated in one part is used in subsequent parts.

 

Self-Check 5

 

SC 5. Four friends stop at a restaurant for its lunchtime pizza special. There is a base price for the pizza and a charge for each topping. Kaz ordered a ham-and-pineapple pizza and paid $10. Leona had the same size of pizza with pepperoni, mushroom, bacon, and black olives. She paid $15.

1. Create a graph of cost versus number of toppings.
2. What does the slope of the graph represent?
3. What is the y-intercept, and what does it represent?
4. Find the equation that represents this situation.
5. Ramon had a pizza with five toppings. How much did he pay?
6. Maggie has $24 to spend. What is the maximum number of toppings she could have?

Compare your answers.

 

Try This 12

 

Complete the following in your binder.
Go to your textbook now to practise applying the concepts that you have learned.

Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 12. a. Complete “Exercises” questions 14 and 16 on page 363.

           b.   Complete “Exercises” question 16 on page 384.
Use the link below to check your answers to Try This 12.
Possible TT12 Solutions

Mathematics 10C Learn EveryWare © 2010 Alberta Education