Lesson 1: Explore | MoodleHUB 🎓

1. Lesson 1

1.5. Explore

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

Explore

Problems involving more than one triangle that share sides are very common. Using shared sides in triangles is, in fact, the core of triangulation used in map-making. If there is not enough information in a triangle to solve it, then a second triangle that shares one side is often used. Consider the following example.

Giovanni and Nakato work for a surveying company and they have been asked to survey the route for a new road. They need to determine the distance from point A to point D where the road will be constructed (marked as b on the following diagram). Unfortunately, this route goes through the middle of some marshland that is very wet, and they cannot directly measure between points A and D. Giovanni measured the distance between points C to B and ∠C and ∠ABD.

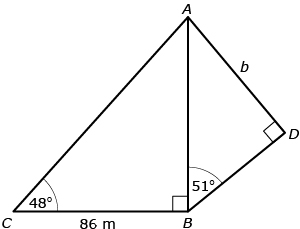
This is a picture of two right triangles: triangle ABC and ABD share side AB. In triangle ABC, side AC is the hypotenuse whose length is unknown, side CB has a length of 86 m, and side AB (shared with the second triangle) has an unknown length. Angle B equals 90 degrees and angle C equals 48 degrees. In triangle ABD, side AB is the hypotenuse whose length is unknown, and side AD is labelled b. Angle D equals 90 degrees and angle B equals 51 degrees.

Giovanni has created a problem where two triangles share a side. can be used as a first step in solving for side b in . Nakato decided to solve for the length of side AB and then used that to solve for the length of side b. Here is her solution for the length of AB:

	Nakato chooses to use the tangent ratio.
	Multiply both sides by 86 as a first step in isolating AB.
86(tan 48°) = AB	The number 86 is cancelled on the right side.
AB = 95.5126...	Nakato has not rounded this number because it is not the final answer to this problem.

Nakato continues, being sure to use her unrounded answer for the length of AB. The following is Nakato’s solution for the length of side b.

	Nakato is writing AB instead of 95.5126... so she remembers to use the unrounded length of AB (see below).
	Multiply both sides by AB in order to isolate b.
AB(sin 51°) = b	AB is cancelled on the right side.
(95.5126...) (sin 51°) = b	Now Nakato replaces AB with the unrounded value calculated above. Calculators often have an ANS key to signify the last calculated number. In this case, Nakato could enter ANS (sin 51°) in her calculator.
b = 74.2272...	The unrounded value of b is 74.2272...
b = 74.2 m	Unless stated otherwise, round distances to the nearest tenth.

Although these examples have concentrated on problems involving triangulation, multiple triangle problems show up in other areas where distances cannot be measured directly. You will work with some of these areas in the following Self-Check.