1. Lesson 2

1.5. Explore 2

Mathematics 20-2 M1 Lesson 2

Module 1: Trigonometry

 

The sine law can be used to solve for side lengths in triangles, such as in the following example.

 

Khadija is building a walkway from her back door to a shed at the back of her yard. She needs to provide the length to a contractor in order to get a phone estimate for the cost. She knows her house is 10.7 m wide and has measured two angles as shown in the following diagram.

 

 

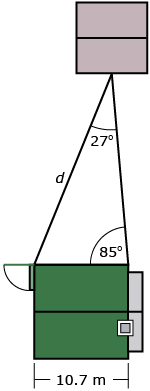
This picture shows Khadija’s house and shed, and the measurements she has made. The house is a square 10.7 m wide with a door at the upper left corner. Immediately above the house is a triangle that shares a horizontal line with the back of the house. The bottom right angle is 85 degrees, the bottom left angle is unknown, and the upper angle is 27 degrees. The side across from the 85 degree angle is labelled d.

 

Khadija can use the sine law to determine the distance from her house to the shed (d on the diagram).

 

 

 Write the sine law using a side-angle pair that you know and the side-angle pair with your unknown distance.

 

 Multiply both sides by sin 85° in order to isolate d.

 

 Cancel sin 85° to isolate d.

d = 23.4791… m

 

 The unrounded value of d is 23.4791...

d = 23.5 m

 

 Unless stated otherwise, distances should be rounded to the nearest tenth.

 


textbook

Read “Example 1: Using reasoning to determine the length of a side” on page 134 of your textbook. As with the preceding example, Elizabeth is not working with a right triangle, so the primary trigonometric ratios cannot be used. Notice how Elizabeth was careful to pair sides with the angles across from them.

 

Ensure that you are comfortable with the steps in this solution before moving on.