Lesson 3

Self-Check 1

 

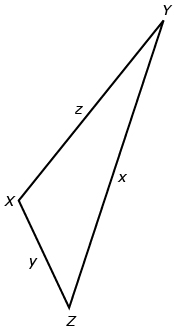
Given the following triangle, state three different ways the cosine law can be written, depending on which angle you are working with.

 

 

Answer

---

Example 1

 

The cosine law can be used to solve the problem given in the Focus section.

 

 

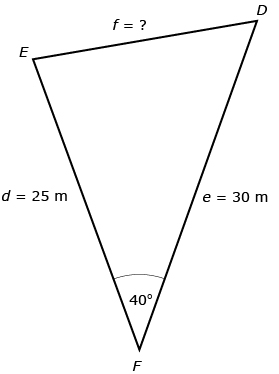
To use the cosine law, you could perform the following steps:

 

f2 = d2 + e2 − 2(d)(e) cos F	Start by stating the correct cosine law for the question.
f2 = 252 + 302 − 2(25)(30) cos 40°	Remember that the angle in the equation is the one across from the side you’re trying to determine. In this example, ∠F is across from the side you are trying to determine.
f2 = 375.9333…	Some students enter the equation above in more than one step (often incorrectly). Remember that your calculator can deal with complicated expressions. Just enter the equation above exactly as you see it.
	You must use the unrounded answer from the previous step. Many calculators let you do this using the ANS key, which stands for “Answer from previous step.”   For some calculators, you would enter . Consult your calculator manual if you can’t find the ANS key on your calculator.
f = 19.3890…	The unrounded value of f is 19.3890…
f = 19.4 m	Round the final answer to one decimal place unless instructed otherwise.