1. Lesson 3

1.5. Explore 4

Mathematics 20-2 M1 Lesson 3

Module 1: Trigonometry

 
Self-Check 3
 

Given the following triangle, state three different ways the cosine law can be written when all three sides are given and you are solving for unknown angles.

 

 

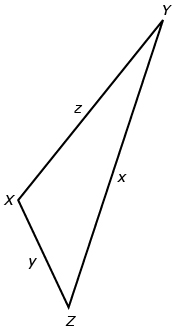
This is an oblique triangle with sides x, y, and z and angles X, Y, and Z.

 

Answer

Example 2

 

This is a photo of a girl holding a compass while standing at the edge of a lake.

David De Lossy/Photodisc/Thinkstock

 

Sandra is taking the same orienteering course as Jeremy in Lesson 2. Sandra is standing at Checkpoint C and knows distances to two other checkpoints, as shown in the diagram. In order to walk in the correct direction, she needs to determine the angle between Checkpoint A and Checkpoint B (θ on the diagram).

 

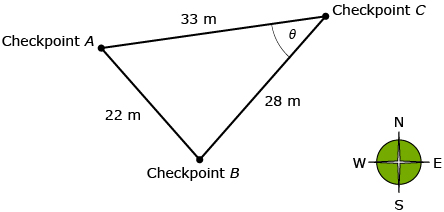
This picture shows an oblique triangle with vertices labelled Checkpoint A, Checkpoint B, and Checkpoint C. The angle at C is labelled theta, side AC is 33 m, side AB is 22 m, and side BC is 28 m.

 

Sandra uses the cosine law to determine angle θ.

 

Write a correct version of the formula.

For this problem, angle θ is across from the side that is 22 m long. Sandra replaces C in the formula with θ because that’s how it’s labelled in her diagram.

cos θ = 0.7516…

Caution: When entering fractions on a calculator, extra care must be taken with brackets. The easiest approach is to always put the numerator in brackets and the denominator in brackets. For this example, you would enter the following in your calculator:

θ = cos−1(0.7516…)

Use inverse cosine (cos−1) to determine θ.

θ = 41.2688…°

The unrounded value of θ is 41.2688…°

θ = 41°

Remember to round to the nearest degree unless instructed otherwise.