Lesson 1

Discover

 

Strategies for solving a puzzle or winning a game can be quite different. One strategy is not necessarily better than the other. Each strategy has its own strengths and weaknesses. In fact, participants may change their strategy several times throughout a game based on their own or an opponent’s performance.

 

Try This 1

 

You should place your completed Try This activities in your course folder. Your teacher may ask to see your completed Try This activities. For more information on Try This activities, refer to the Course Introduction.

 

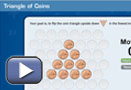
Arrange 10 coins to create a triangle as shown in the diagram. Alternatively, you can use the Triangle of Coins applet.

 

• Manipulate the coins one by one to turn the triangle upside down so the point faces down.
  
  
• What is the minimum number of moves to flip the triangle upside down?

Place a description or sketch of your strategy in your course folder. In your sketch, be sure to identify which coins you moved and where you moved them to. You may want to use arrows to identify specific movements or take a video of your manipulations of the coins.

 

Share 1

 

After a discussion with your teacher, you will decide how to connect with other students for Share activities. Follow your teacher’s instructions to complete this Share activity. Place a summary of your Share discussion in your course folder. For more information on Share discussions, refer to the Course Introduction.

 

Compare your strategy for flipping the triangle of coins with another student or partner. This may be done in person or virtually. For instance, you may want to post your response to the discussion board or have a video conference with another student.

 

In your discussion answer the following questions:

• How were the strategies similar?
  
  
• How were the strategies different?
  
  
• Were both strategies successful? In other words, was the final orientation a triangle that pointed downwards?
  
  
• Who had the lowest number of moves to flip the triangle?

When you compared your strategies for flipping the triangle of coins, did you determine that the minimum number of moves required is three? If not, you may want to go back and revisit your approach.

 

In the triangle puzzle, a strategy that took three moves would be more successful than a strategy that took five moves. The success of a strategy in this case is based on the number of moves required to complete the puzzle. For some games and puzzles, the number of moves is not crucial. What is important is solving the puzzle. This can be achieved using various strategies.