1. Lesson 3

1.9. Lesson 3 Summary

Module 2: Lesson 3

Module 2: Logic and Geometry

 

Lesson 3 Summary
 

In Lesson 3 you looked at how logical reasoning can be used to prove conjectures made about games and puzzles. Deductive reasoning uses a well-developed system of logic to prove a conjecture.

 

You begin by making a conjecture—this is usually based on observation. Inductive reasoning is used to develop a rule or generalization from a conjecture. Remember that inductive reasoning moves from the specific to the general. You then use deductive reasoning to show that the generalization can be applied to all possible cases, which, logically proves conjectures.

 

For instance, Wahid made a conjecture in this lesson for describing the triangular arithmagons. The conjecture was expressed as a general statement that can be applied to all triangular arithmagons. Wahid’s group then proved that its generalization was valid for all triangular arithmagons, as shown in the following proof.

 

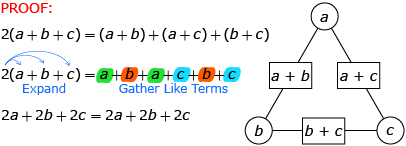
This is a graphic of showing the proof for triangular arithmagons.

 

Remember that deductive reasoning is the opposite of inductive reasoning. Inductive reasoning starts with specific assumptions and concludes something general. Deductive reasoning starts with general statements that are assumed to be true and derives specific conclusions.

 

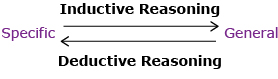
This is a graphic showing an arrow going from specific to general. The words “inductive reasoning” are placed above the arrow. Another arrow going from general to specific has the words “deductive reasoning” placed below it.

 

Proofs can take on a variety of forms. They may involve algebra, Venn diagrams, or tables that relate statements and justifications (e.g., two-column proofs). The strategy used to prove a conjecture using deductive reasoning will depend on the conjecture as well as the personal strategy of the person writing the proof.

 

When deductive reasoning is used correctly, you can be sure that the conclusion you draw is valid. However, proofs arrived at by deductive reasoning can be invalid if the reasoning is flawed. In Lesson 4 you will further investigate deductive reasoning and learn how to identify when the reasoning contains an error.