Lesson 4: Explore | MoodleHUB 🎓

1. Lesson 4

1.2. Explore

Mathematics 20-2 M2 Lesson 4

Module 2: Logic and Geometry

Explore

invalid proof: a proof that contains invalid assumptions or has an error in reasoning1

Earlier in this module, you learned that conjectures based on inductive reasoning may be valid for specific examples but cannot be proven. It is impossible to look at all possible cases. Conjectures can be weakened by insufficient evidence or by ignoring counterexamples (e.g., only testing those cases that you know support the conjecture). Conjectures can also be invalidated by a single counterexample. In a similar way, proofs can be invalidated if there are errors in the proof or if invalid assumptions are used when developing the proof. In Lesson 3 you learned how deductive reasoning can be used to prove conjectures. However, not all proofs are valid. Joel’s Solution is an example of an invalid proof.

Joel’s proof contained an error. In his solution, Joel did not divide both terms in the numerator by the term in the denominator.

Joel’s Solution

Let n represent any integer.

Let n + (n + 1) + (n + 2) + (n + 3) represent a sum of 4 consecutive integers.

So, represents the sum of the 4 consecutive integers divided by the number of integers in the set (4).

I can simplify this as shown:

This is a graphic showing Joel’s conjecture with “invalid” written overtop.

Since 4n can be divided by 4, this proves that the sum of four consecutive integers is evenly divisible by the number of terms.

Dividing both terms in the numerator by the denominator results in n + 1.5.

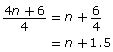
Since 6 is not evenly divisible by 4, this counterexample disproves the conjecture that the sum of an even number of consecutive integers is evenly divisible by the number of integers.

Sometimes the identification of an error in a proof can be used to correct mistakes in a proof.

Read “Example 4: Using reasoning to determine the validity of a proof” on page 40 of your textbook to see a situation where correcting a mistake made the proof valid.

You probably noticed that Joel and Hossai made the same type of error. Each forgot to divide both of the terms in the polynomial by the divisor. However, correcting the error had very different results. It is important to review each step of your proof for errors before you declare whether it is valid or not.