1. Lesson 6

1.5. Explore

Module 2: Lesson 6

Module 2: Logic and Geometry

 

Explore
 
This is a photo of two students looking at a laptop computer.

iStockphoto/Thinkstock

Inductive reasoning has been used in this lesson to develop conjectures about the relationships between angles and intersecting lines. As you have seen in previous lessons, inductive reasoning begins with specific assumptions and concludes with something general. These conclusions may or may not be true for all cases. In fact, you should recall that only one counterexample is enough to make the conjecture invalid.

 

In the Try This activities, you made conjectures about the relationships between pairs of angles formed by intersecting lines using inductive reasoning. For instance, in Try This 1 you may have made the conjecture that opposite angles are congruent or equal in measure. You can go back to Try This 1 and use the Opposite Angles applet to review your conjecture.

 

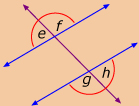
In Try This 2 and Try This 3, you observed relationships between angles formed when a transversal intersects two lines. Rozanna and Josh also made conjectures based on the relationships they observed between the measures of the interior angles and exterior angles in Try This 2 and Try This 3.

 

interior angles: angles that are located between two lines intersected by a transversal

 

 

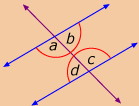
This illustration shows interior angles.

 

exterior angles: angles that are located outside two lines intersected by a transversal

 

 

This illustration shows exterior angles.


 

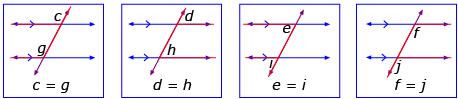
Based on her observations, Rozanna made the following conjecture: When a transversal intersects two parallel lines, the corresponding angles are always equal.

 

corresponding angles: angles that are in the same position relative to lines intersected by a transversal

 

One way to find corresponding angles is to draw the letter F on the diagram. This can be forwards, backwards, and even upside down.

 

 

This illustration shows corresponding angles.


 

Rozanna supported her conjecture with the following diagrams.

 

This is an illustration showing that when a transversal intersects a pair of parallel lines, the corresponding angles formed by each parallel line and the transversal are equal.

 

converse: a statement that is formed by switching the premise and the conclusion of another statement1

Josh said that the converse of Rozanna’s conjecture was also true. He concluded that when a transversal intersects two lines and creates corresponding angles that are equal, the two lines are parallel. Josh’s conjecture switches Rozanna’s premise about equal corresponding angles with her conclusion that the lines are parallel.

 

Rozanna’s conjecture is that when a transversal intersects two parallel lines, the corresponding angles are always equal. Josh’s conjecture is that when a transversal intersects two lines and creates corresponding angles that are equal, the two lines are parallel.

1 Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 71. Reproduced by permission.

 

You may want to verify Rozanna’s and Josh’s conjectures using the Angles and Lines animation. (You first used this multimedia item in Try This 2.) Can you find any counterexamples for their conjectures? Also, consider whether Rozanna’s and Josh’s conjectures can be expanded to include non-parallel lines. In other words, are corresponding angles equal when a transversal intersects a pair of non-parallel lines?

 

 

This is a screenshot for Angles and Lines.