1. Lesson 6

1.6. Explore 2

Module 2: Lesson 6

Module 2: Logic and Geometry

 

Self-Check 1
 

In each diagram, is CD parallel to EF? Explain how you know.

 

a. 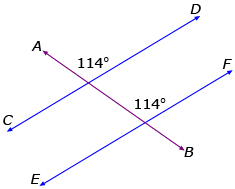This is a graphic of transversal intersecting parallel lines. Two corresponding angles both measure 114 degrees.
Answer

 

 

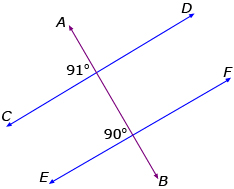
b. This is a graphic of transversal intersecting lines. Two corresponding angles are shown. One angle measures 91 degrees, and the other angle measures 90 degrees.
Answer

Sue also observed some relationships between pairs of angles formed by transversals and parallel lines. Based on her observations from Try This 2 and Try This 3, Sue concluded that the interior angles on the same side of a transversal that intersects a pair of parallel lines are supplementary. (Supplementary angles add up to 180°.) These are sometimes referred to as consecutive interior angles because they are next to one another. A quick way to find these angles is to draw the letter C on the diagram (either backwards or forwards).

 

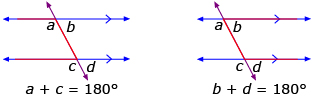
This is a graphic showing that the interior angles on the same side of a transversal that intersects a parallel line are supplementary.

Self-Check 2
 

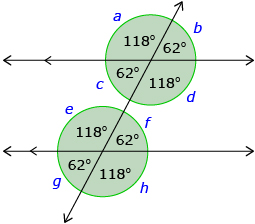
There are a number of pairs of supplementary angles in addition to consecutive interior angles.

 

Identify the supplementary angles in the following diagram. Answer

 

This is a graphic of two parallel lines interested by a transversal. The measures of all eight angles formed by the three lines are given in the diagram. Angles a and e are both 118 degrees. Angles b and f are 62 degrees. Angles c and g are 62 degrees. Angles d and h are 118 degrees.

Instead of using the Angles and Lines applet and the Parallel Lines applet to gather evidence, Quinn decided to use a protractor to measure the angles formed by the intersecting lines on the fox and geese game board. Quinn focused on the relationship between alternate angles on the game board. Specifically, he considered the alternate exterior angles.

 

alternate angles: two non-adjacent angles on opposite sides of a transversal

 

There are alternate interior angles and alternate exterior angles. Alternate angles form a Z shape.

 

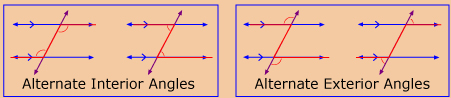
This illustration shows alternate angles.

 

alternate exterior angles: two exterior angles formed between two lines and a transversal, on opposite sides of the transversal

 

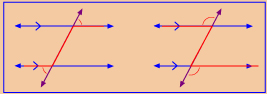
This illustration shows alternate exterior angles.


 

Watch the animation Angles of Play to see the evidence Quinn collected and the conjecture he developed based on his evidence.

 

 

This is a screenshot for Angles of Play.