1. Lesson 7

1.2. Explore

Module 2: Lesson 7

Module 2: Logic and Geometry

 

Explore
 

Did You Know?


This is a photo of pottery with geometric designs.

Hemera/Thinkstock

 

Archaeological evidence shows that ancient Americans applied their knowledge of the principles of geometry to architecture and city planning. These principles are also seen in the ornamental designs that were used in sculpture, painting, and textile patterns, such as those woven by the Maya for hundreds of years.

 

— Emory Dean Keoke, Kay Marie Porterfield. Encyclopedia of American Indian Contributions to the World.
(Facts on File, 2001.) p. 118.

There are many situations where it is important that lines are parallel. The success of designs ranging from railings on stairs to geometric designs on pottery to rehabilitation equipment is dependent on angle properties. Thus, it is crucial that the angle properties being used in the design are proven to be true.

 

This is a photo of a senior using parallel bars to walk with a physical therapist.

Photodisc/Thinkstock


 

theorem: a statement that has been accepted as true

Recall from earlier in this module that a proof involves deductive reasoning. In a proof, a specific conclusion is drawn through logical reasoning by using general assumptions that are known to be valid. These assumptions or statements that are accepted as true and used to prove a particular statement or conjecture are sometimes called theorems or properties.

 

A variety of strategies can be used to prove a conjecture. Sketching a figure that illustrates the situation you are trying to prove is a useful starting point. The diagram can then help you to develop a plan and identify the specific relationships or assumptions you need to include in your proof. You may find that working backwards can help you to identify the relationships and their corresponding statements. Ask yourself questions like, “If the statement I want to prove is valid, what else would have to be valid in my diagram?”

 

This is an illustration of a thought bubble containing the question, “If the statement I want to prove is valid, what else would have to be valid in my diagram?”

Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11 TR, © 2012 Nelson Education
Limited. p. 82. Reproduced by permission.

 

Organizing the statements in two columns is one way of presenting the proof. This approach is known as a two-column proof. In Lesson 3 you learned that the left-hand column of a two-column proof contains the statements presented in a logical order. The right-hand column of the table has the reasons for or justifications of why each of the statements is valid.

 

 

This is a graphic of a table with two columns. The left-hand column is labelled statement and the right-hand column is labelled justification.

 

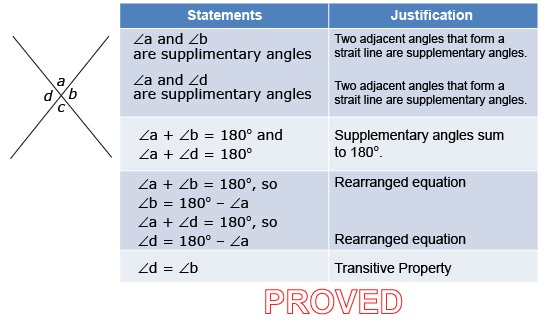
Consider the following situation. Gilles decides to use a two-column proof to prove that the vertically opposite angles are equal in the supporting poles of a trapper’s tent that is set up at a local gathering.

 

Watch the animation Gilles’s Proof to see how Gilles uses deductive reasoning to prove that vertically opposite angles are equal.

 

 
This is a screenshot for Gilles’s Proof.
 

Alberta Economic Development

 

transitive property: if two quantities are equal to the same quantity, then they are equal to each other

 

If a = b and b = c, then a = c.

 

— CANAVAN-MCGRATH ET AL. Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 29.
Reproduced by permission.

In his proof, Gilles used a diagram to visualize the situation. He used the diagram to reason through the proof. Then he recorded the statements and their justifications in the table. One of his statements in his table was justified by the transitive property. The transitive property says that if two quantities are equal to the same quantity, then they are equal to each other.

 

Prove ∠d = ∠b.

 

 

This is an illustration of two intersecting straight lines and a two-column proof.

 

Remember that the purpose of a proof is to show that the conjecture is true in all cases. The specific strategy that is used for a proof will vary based on the conjecture and the individual’s personal strategy for creating the proof.


textbook

Read “Example 1: Reasoning about conjectures involving angles formed by transversals” on pages 75 and 76 of your textbook. In this example, two different personal strategies are used to prove two conjectures.

  • In the first, Tuyet proves that alternate interior angles are equal when a transversal intersects a pair of parallel lines.

  • In the second, Ali proves that interior angles on the same side of the transversal are supplementary when a transversal intersects a pair of parallel lines.

As you read through the two different proofs, consider the similarities and differences in each person’s proof. For instance, in the first solution, Tuyet uses a two-column proof. In the second solution, Ali writes out an explanation of what she did at each step of the proof to demonstrate her reasoning.