Lesson 7
1. Lesson 7
1.3. Explore 2
Module 2: Logic and Geometry
Self-Check 1
Complete “Check Your Understanding” question 2 on page 78 of the textbook. Answer
Self-Check 2
Use the following applet titled Self-Check 2 to prove that alternate exterior angles are equal.

Comstock/Thinkstock
When deductive reasoning is used correctly in a proof, you can be sure that the conclusion drawn is valid. If any error occurs, the proof is invalid. Given that many designs are based on the application of angle properties, it is crucial to the success of the designs that errors do not exist in the reasoning behind the designs.
For instance, the design for a cellphone tower is shown in “Example 3: Using angle properties to prove that lines are parallel” on page 77 of your textbook. The design requires parallel braces for the tower. In this example, Morteza and Jennifer used different pairs of angles to prove that the braces on the cellphone tower are parallel.
Read over each proof in Example 3 on page 77 of your textbook. As you examine the proofs, consider what properties of angles each girl used for their proof. A summary of the angle properties related to the angles formed when a transversal intersects two parallel lines is provided.
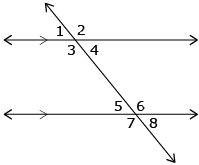
The lines are parallel if a transversal intersects two lines and the following occurs:
- The corresponding angles are equal: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, and ∠4 = ∠8.
- The alternate exterior angles are equal: ∠1 = ∠8, and ∠2 = ∠7.
- The alternate interior angles are equal: ∠3 = ∠6, and ∠4 = ∠5.
- The interior angles on the same side of the transversal are supplementary: ∠3 + ∠5 = 180°, and ∠4 + ∠6 = 180°.