1. Lesson 8

1.5. Explore 2

Mathematics 20-2 M2 Lesson 8

Module 2: Logic and Geometry

 
Lesson Assignment


 
assignment

Complete question 1 of your Lesson 8 Assignment that you saved to your course folder. Then resave your updated Lesson 8 Assignment to your course folder.

 



Geometric designs containing parallel lines are evident in many cultures. These designs can be found in paintings on rocks, etchings in the ground, baskets, pottery, textiles, beadwork, and ceremonial pieces. For example, in the Democratic Republic of the Congo, the Mangbetu women wore pieces of barkcloth that were decorated with geometric patterns like the one shown.

 

This illustration shows an example of a pattern from a barkcloth.

 

Did You Know?


The Mangbetu ideal of feminine beauty included painting the body in geometric patterns. The women of the ruling class painted their bodies with a black juice made from the gardenia plant.

— Paulus Gerdes. Geometry from Africa: Mathematical and Educational Explorations. (Washington: Mathematical Association of America, 1999). Pp. 25, 29.


 

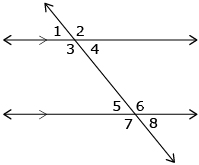
This illustration shows that angle properties that must exist for two lines to be parallel when intersected by a transversal.

To create a successful final product, some designs need the lines to be parallel. Designers can verify that the lines they construct in their designs are parallel by measuring the angles formed by the lines and a transversal. A review of the angle relationships formed when a transversal intersects two parallel lines is provided on the right. Remember, it does not matter if the lines look parallel; they have to be parallel for the angle properties to apply.

 

The lines are parallel if a transversal intersects two lines and the following occurs:

  • the corresponding angles are equal: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8
  • the alternate exterior angles are equal: ∠1 = ∠8 and ∠2 = ∠7
  • the alternate interior angles are equal: ∠3 = ∠6, ∠4 = ∠5
  • the interior angles on the same side of the transversal are supplementary: ∠3 + ∠5 = 180°,
    ∠4 + ∠6 = 180°
This illustration shows an example of a pattern used to decorate gourds in Nigeria.

Consider the following situation. Akono is taking a pottery class. One of his projects is to decorate a serving plate with a geometric design. He decided to use a pattern he found in his research that was used to decorate gourds in Nigeria.

 

Akono wants to check that the lines he constructed on his serving plate are parallel. Using a protractor, Akono measures some of the angles on the completed plate. Watch the animation Measuring Angles in Akono’s Design to see the angle measurements.

 

 

This is a screenshot for Measuring Angles in Akono’s Design.

 

Akono’s reasoning used the property of corresponding angles to prove that the lines that he selected in his design are parallel.